Co to jest logarytm?
Jeżeli mamy zależność:
ab = c
to znając
a oraz c, szukamy takiego b, które spełni nasze równanie. Zapisujemy
to:
b = loga c
- odczytujemy jako "b równy jest logarytmowi z c przy podstawie
a"
We wzorze a jest nazywane "podstawą logarytmu".
Logarytm jest funkcją odwrotną do podnoszenia do potęgi o zadanym
wykładniku.
Podstawowe zależności (własności) logarytmów, wynikające z
definicji.
logm 1 = 0 logarytm z jedynki (przy dowolnej
podstawie) równy jest zero.
logm m = 1
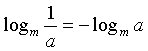
Podstawa logarytmu
Logarytm może mieć dowolną podstawę różną od 1. Są jednak
pewne szczególnie ważne w matematyce i technice podstawy logarytmu.
Logarytm dziesiętny
Podstawą logarytmu najczęściej jest liczba 10 (mówimy wtedy o
logarytmie dziesiętnym). Zapisujemy go po prostu jako log c (bez
wypisywania podstawy).
log10 c = log c
logarytm naturalny
Innym ważnym logarytmem jest logarytm naturalny, którego podstawą
jest liczba niewymierna oznaczana literą e. Wartość e
przekracza nieco 2,7 (kto chce poznać więcej miejsc po przecinku niech
otworzy sobie windowsowy kalkulator w widoku "naukowym" i wciśnie
po kolei 1, "inv". "ln" - czyli wciskamy jedynkę,
zaznaczamy pole "inv" oraz klikamy przycisk "ln").
Znaczenie logarytmu naturalnego ujawnia się przy posługiwaniu się
rachunkiem różniczkowym i całkowym.
Logarytm naturalny oznaczamy (przynajmniej w Polsce, bo anglosasi
miewają to inaczej) przez ln:
loge b = ln b
Wzory z logarytmami
Definicja:
b = loga c , jeśli:
ab
= c
logarytm iloczynu i ilorazu:
logm a·b = logm a +
logm b
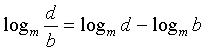
logartym potęgi:
logm ab = b· logm a
Oczywiście wzory powyższe obowiązują oczywiście w ich dziesiętnej
i naturalnej odmianie np.:
log a·b = log a + log b,
ln a·b = ln a + ln b ,
log ab
= b· log a,
ln ab = b·
ln a itp.
|
![]()
![]()