Wzory z matematyki
|
Kombinatoryka
|
silnia
|
n! = 1·2·3·4·...·(n-1)·n
Przykład: 5! = 1·2·3·4·5
= 120
|
Symbol Newtona
|
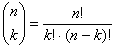
Przykład:
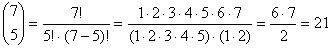
Więcej informacji na ten temat znajduje się w rozdziale Symbol
Newtona
|
Dwumian Newtona
|
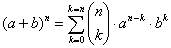
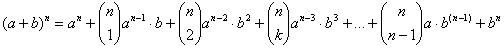 |
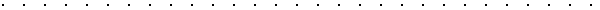
Obliczenia kombinatoryczne
|
Wariacje z powtórzeniami
k wyrazową wariacją z powtórzeniami ze n-elementowego
zbioru (n > k) nazywamy każdy k wyrazowy ciąg elementów
z tego zbioru.
Przykład:
Wariacją 3 elementową z 24 elementowego zbioru byłby każdy wyraz
(sensowny, prawdziwy, lub nie) jaki daje się ułożyć z 24 liter
podstawowych alfabetu. Wchodziłyby tu takie wyrazy jak ala, aaa, huk, bbu
tip.
|
Ilość k wyrazowych wariacji z powtórzeniami równa jest:
nk
Przykład:
Ilość wariacji (możliwych ułożeń wyrazów) dla przykładu z wyrazami
liter alfabetu - jak obok wyniesie: 243 = 13 824.
|
Wariacje bez powtórzeń
k wyrazową wariacją bez powtórzeń z n-elementowego
zbioru (n > k) nazywamy każdy k wyrazowy ciąg elementów,
którego wyrazy są różnymi elementami z tego zbioru.
Przykład:
Wariacją 3 elementową bez powtórzeń z 24 elementowego zbioru byłby każdy
wyraz (sensowny, prawdziwy, lub nie) jaki daje się ułożyć z 24 liter
wybranych z kompletu scrabble. W odróżnieniu od przykładu dla wariacji
z powtórzeniami, tutaj nie da się w tym samym wyrazie użyć drugi raz
tej samej litery.
|
Ilość k wyrazowych wariacji bez powtórzeń
równa jest:
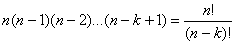
Przykład:
Ilość możliwych ułożeń wyrazów 3 literowych z 24 liter scrabble jest
równa:
24 · (24-1) · (24 -2) = 24 · 23 · 22
= 12 144
|
Permutacje bez powtórzeń
Permutacją bez powtórzeń n - elementowego zbioru nazywamy każdy
ciąg (n - elementowy) zawierający wszystkie elementy z
tego zbioru.
Przykład:
Permutacją 3 elementową bez powtórzeń byłoby każde ułożenie w wyraz
3 literek wyciągniętych z kompletu scrabble. Zakładamy, że literek tych
nie da się wymieniać na inne.
|
Ilość permutacji bez powtórzeń wynosi
n!
Przykład:
Ilość możliwych ułożeń wyrazów z 3 liter scrabble jest równa:
3! = 1 · 2 · 3 = 6 |
Kombinacje bez powtórzeń
k elementową kombinacją bez powtórzeń
zbioru A nazywamy:
każdy k elementowy podzbiór zbioru A.
Przykład:
Kombinacją 5 elementową bez powtórzeń ze zbioru 7 elementowego byłoby
każde wylosowanie 5 literek wyciągniętych z woreczka scrabble zawierającego
7 (różnych) literek. Zakładamy, że nie interesuje nas kolejność
losowania (czy tez ustawiania w ciąg) tych liter i dlatego wyciągnięcie
"a" za pierwszym, drugim, czy innym razem jest traktowane jako to
samo losowanie, o ile tylko pozostałe litery w wylosowanym zestawie będę
też takie same. |
Ilość k elementowych kombinacji zbioru zawierającego n
elementów dana jest symbolem
Newtona, czyli wynosi:
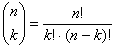
Przykład:
Ilość możliwych wyciągnięć (różnych) literek z woreczka scrabble
zawierającego 7 kostek wynosi:
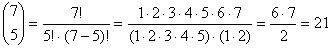
|
|
![]()
![]()