|
|
Układ odniesienia - wstępTreści powiązane z tym rozdziałem: wektory i skalary Mechanika, a w szczególności Pierwsza zasada dynamiki Newtona (także np. teoria względności) posługuje się pojęciem układu odniesienia. Cóż to takiego?
Jednak układ odniesienia możemy związać z czymś innym – np. właśnie z lecącym samolotem. W układzie odniesienia związanym z samolotem w ruchu jest Ziemia, dom, góra; ale teraz sam samolot oraz jego fotele, kokpit, kadłub i śpiący pasażerowi pozostają w spoczynku. Tu trzeba się wyzbyć pewnego przyzwyczajenia umysłu, aby zaakceptować ważny fakt, że: Wszystkie (poprawnie określone) układy odniesienia są jednakowo „prawdziwe”. Np. w sensie fizycznym bez sensu jest stwierdzenie, że „tak naprawdę” przecież dom się nie porusza, bo stoi na Ziemi. Nie porusza się względem Ziemi i wszystkich innych przedmiotów, które nie poruszają się względem naszego globu. Jednak poruszają się względem lecącego samolotu, a także Księżyca, Słońca (które jest znacznie większe i cięższe od Ziemi), Galaktyki oraz miliardów innych obiektów znacznie masywniejszych i „ważnych” z kosmicznego punktu widzenia niż stosunkowo niewielka planeta Ziemia. Układ odniesienia ma jeszcze inne ważne właściwości - może on posłużyć jako baza do wykonywania pomiarów. Bo ustanawia on nam jakby zbiór „zer” i jednostek dla fizycznego laboratorium. Chodzi tu o:
Kartezjański układ współrzędnychNa schematach układ odniesienia rysuje się najczęściej jako układ dwóch osi XY, lub trzech osi XYZ. Jest to tzw. układ współrzędnych kartezjańskich (nazwany od nazwiska słynnego uczonego francuskiego Rene Descartes, zwanego też Kartezjuszem).
Poza tym, aby układ był kompletny, określa się jednostki na osiach (i ew. jednostkę czasu). Najczęściej więc położenie wyrażane jest metrach, czas w sekundach. Stąd wynikają w sposób naturalny jednostki prędkości - m/s. Jednak w razie potrzeby jednostki można zmienić na bardziej wygodne. Czas absolutny, czy względnyMechanika klasyczna (niutonowska) posługuje się pojęciem absolutnego czasu, czyli czasu płynącego identycznie we wszystkich układach odniesienia. Teoria względności odrzuca założenie czasu absolutnego, ponieważ doświadczenia związane z obserwacją biegu promieni świetlnych nie dają się pogodzić z tą ideą. W zamian wprowadza się czas, który biegnie różnie w różnych układach odniesienia.
Układ odniesienia - podsumowanie:Układ odniesienia służy do ustalenia, wtedy możemy powiedzieć kiedy prędkość jakiegoś obiektu wynosi zero, kiedy położenie jest zero i którą chwilę czasu ustalimy jako 0. Dzięki temu dostajemy też możliwość określenia wielkości różnych od zera – czyli np. stwierdzenia, że prędkość muchy to 6m/s, a prędkość kota to 2m/s. Są to wszystko prędkości względem naszego układu odniesienia. Więcej informacji na temat zagadnień definiowania układu odniesienia znajduje się w rozdziałach temu poświęconych. Układ odniesienia - patrz także:
|
 Przykładowo układ odniesienia można związać z Ziemią. W tym układzie
Ziemia znajduje się w spoczynku, a wszystkie obiekty poruszające się
względem niej – w ruchu. W ruchu będzie więc lecący samolot (i
fotele zamontowane do tego samolotu), hamujący samochód, lecąca mucha.
W spoczynku względem Ziemi będzie dom, albo góra, która się na tej
Ziemi znajduje.
Przykładowo układ odniesienia można związać z Ziemią. W tym układzie
Ziemia znajduje się w spoczynku, a wszystkie obiekty poruszające się
względem niej – w ruchu. W ruchu będzie więc lecący samolot (i
fotele zamontowane do tego samolotu), hamujący samochód, lecąca mucha.
W spoczynku względem Ziemi będzie dom, albo góra, która się na tej
Ziemi znajduje.
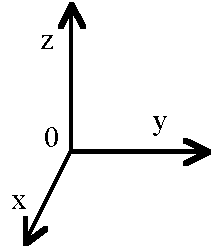 Układ
odniesienia możemy właściwie wybrać dowolnie, ale później należy się
tego wyboru trzymać, bo jeśli go zmienimy to nie będzie to już dokładnie
ten sam układ odniesienia, tylko inny.
Układ
odniesienia możemy właściwie wybrać dowolnie, ale później należy się
tego wyboru trzymać, bo jeśli go zmienimy to nie będzie to już dokładnie
ten sam układ odniesienia, tylko inny.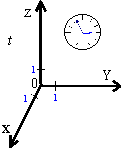 Jeśli
układ współrzędnych jest używany do opisu ruchu, to istotnym staje się
podanie jeszcze jednej zmiennej charakteryzującej sytuację - czasu t.
Jeśli
układ współrzędnych jest używany do opisu ruchu, to istotnym staje się
podanie jeszcze jednej zmiennej charakteryzującej sytuację - czasu t.