|
|
Jak rozumieć II zasadę dynamiki?II zasada dynamiki jest zapisywana najczęściej wzorem: Jak ten wzór rozumieć? II zasada dynamiki Newtona mówi nam o efekcie działania siły na swobodne ciało. Siła nadaje ciału przyspieszenie, czyli zmienia prędkość ciała. W zwykłej postaci II zasadę dynamiki formułuje się dla układów inercjalnych. Oznacza to, że w pełnym brzmieniu można by tę zasadę podać jako: W układach inercjalnych przyspieszenie nadawane przez jakaś siłę jest wprost proporcjonalne do wartości tej siły, a odwrotnie proporcjonalne do masy ciała. |
|
|
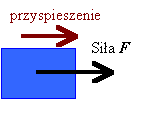
1. Im większa jest siła, tym większe przyspieszenie (większa zmiana prędkości wywołana w zadanym czasie). |
|
|
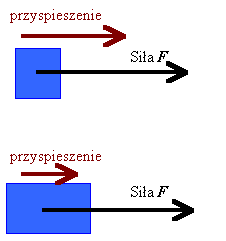
| 2. Im większa jest masa ciała, tym
proporcjonalnie większej siły potrzeba, aby wywołać to samo
przyspieszenie.
II zasada dynamiki określa jak możliwość uzyskania przyspieszenia
przez ciało zależy od masy: |
|
|
Korzyść z zastosowania II zasady dynamiki
objawia się wtedy, gdy dowiemy się, że siła jest wielkością użyteczną
z tego powodu, że dla bardzo wielu sytuacji z góry wiemy jaka jest jej
wartość. Znając zaś tę wartość będziemy teraz mogli przewidzieć
co stanie się z ciałem - czy ono przyspieszy, czy zwolni, a może (jeśli
siły nie działają) zachowa swój stan ruchu (pozostanie w spoczynku,
lub będzie poruszało się ruchem jednostajnym, prostoliniowym).
Niezbyt szczęśliwe ujęcie II zasady dynamikiCzęsto o II zasadzie dynamiki mówi się w kontekście przekształconej postaci wzoru - zamiast wyliczać przyspieszenie, podaje się wzór na siłę: F = ma Takie podejście nie jest błędem, ale wg mnie stanowi pewną niezręczność przekazu. Bo przecież samo obliczenie wartości F wg tego wzoru niczego specjalnego nam nie mówi o przyrodzie - tu dowiadujemy się tylko, że z pomnożenia wartości m oraz a powstaje wartość określana jako F. Ale co z tego? Prawdziwy sens II zasady dynamiki, to odwołanie się do schematu przyczyna -> skutek. Siła będąca przyczyną zmiany ruchu, powoduje przyspieszenie o wartości a. Właśnie tak jak w podstawowym wzorze:
|
||