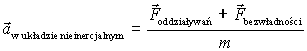|
|
Siła bezwładnościSpis treści rozdziału:1. Wstęp
3. Przykłady sił
bezwładności
5. Inne rodzaje sił bezwładności WstępSiła bezwładności nie jest zwykłą siłą. Właściwie można by nawet powiedzieć, że w ogóle nie jest siłą. Bo nie wynika ona z żadnego oddziaływania między ciałami (a przecież definiowaliśmy siłę jako miarę oddziaływania). Jeszcze inaczej można by powiedzieć, że jest ona siłą pozorną. |
|||||||
|
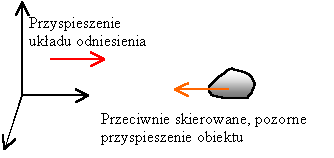
Siła bezwładności jest efektem wynikającym z samego przyspieszenia układu odniesienia. Jeżeli układ odniesienia porusza się ruchem przyspieszonym względem otoczenia, wtedy z jego poziomu ciała w tym otoczeniu też poruszają się ruchem przyspieszonym (tylko skierowanym przeciwnie). Wygląda to tak samo jakby działała na nie jakaś siła. I właśnie sztucznie przypisana temu ruchowi siła jest siłą bezwładności.
Siła bezwładności pojawia się tylko w nieinercjalnych układach odniesienia. Patrz rozdział - układy inercjalne Siła bezwładności, a druga zasada dynamiki NewtonaW układach inercjalnych obowiązuje "normalna" postać II zasady dynamiki Newtona
A w układach nieinercjalnych?
Dlaczego? Siła bezwładności jako poprawka do wzoru II zasady dynamikiMożna jednak poprawić (można by też zamiast
"poprawić", przychylić się do słówka "oszukać")
opis układów nieinercjalnych tak, aby obowiązywała w nich zmodyfikowana
wersja II zasady dynamiki (zamiast "zmodyfikowana", można by
w pewnym sensie powiedzieć "oszukana"). W tym celu do
rzeczywistych sił (a więc sił wynikających z oddziaływań) trzeba dodać
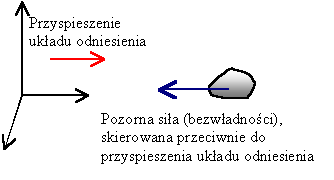
"pseudosiłę" - siłę bezwładności. Wzór na siłę bezwładności
Minus we wzorze bierze się z faktu, że siła bezwładności działa przeciwnie do przyspieszenia układu nieinercjalnego.
Teraz możemy wprowadzić poprawioną (obowiązującą również
w układach nieinercjalnych) II zasadę dynamiki Newtona.
II zasada dynamiki w układach nieinercjalnychA oto wzór zmodyfikowanej II zasady dynamiki (z poprawką na nieinercjalność układu):
I ta poprawiona wersja II zasady dynamiki Newtona dopiero teraz dobrze działa w układach nieinercjalnych. Na koniec możemy jeszcze nazwać sobie sumę siły wypadkowej oddziaływań i siły bezwładności nazywamy siłą całkowitą i oznaczymy (tradycyjnie) przez F, to będziemy mogli w zgodzie z prawdą wypisać taki sam wzór jak w standardowej II zasadzie dynamiki Newtona: Tutaj F jest siłą
całkowitą, Przykłady siły bezwładnościSiły bezwładności pojawiają się w różnych sytuacjach. Oto przykłady:
Chciałbym tu jeszcze raz podkreślić, że: Siłą rzeczywiście działającą na ciało jest siła dośrodkowa, która zakrzywia tor ciała zmuszając je do krążenia po okręgu, a nie poruszania się prostoliniowo. Siła dośrodkowa wynika z istnienia jakiegoś oddziaływania -np. zaczepienia na lince, tarcia, siły grawitacji. Jeszcze jednym istotnym spostrzeżeniem na temat sił bezwładności jest to, że jeśli układ odniesienia jest związany z jakimś obiektem materialnym (pojazdem, karuzelą itp.), to każdej sile bezwładności zawsze towarzyszy jakaś siła oddziaływań, która nadaje temu obiektowi przyspieszenie. |
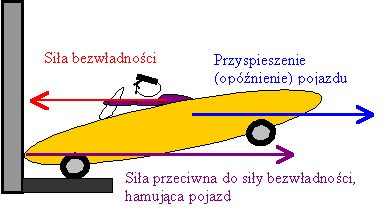
Siły w układach inercjalnych i nieinercjalnych - analiza przykładowych sytuacjiAby lepiej zrozumieć czym jest siła bezwładności prześledzimy dwie dość typowe sytuacje opisu ruchu w układzie inercjalnym i nie inercjalnym. Sytuacja 1 – hamujący samochódHamujący samochód podlega działaniu siły hamowania skierowanej przeciwnie do kierunku ruchu. W wyniku działania tej siły samochód uzyska przyspieszenie skierowane przeciwnie do prędkości.
Opis sił działających na kierowcę w układzie inercjalnym.W układzie inercjalnym widzimy sytuację z zewnątrz (np. jako obserwator patrzący na samochód z chodnika). Widzimy, że samochód ma malejącą prędkość i przyspieszenie skierowane przeciwnie do tej prędkości. |
|||||||||
|
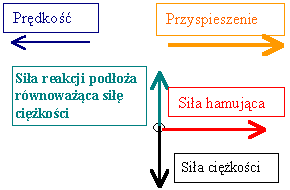
Da się tu wyróżnić 3 siły działające na kierowcę:
|
 |
||||||||
|
Narysuję te siły jeszcze raz sprowadzając ludzika do punktu. W układzie inercjalnym mamy siłę wypadkową równą sile hamującej. Nadaje ona samochodowi i kierowcy opóźnienie (przyspieszenie skierowane przeciwnie do prędkości). II zasada dynamiki Newtona ( |
 |
||||||||
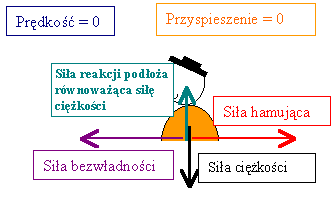
Opis tej samej sytuacji w układzie nieinercjalnym, związanym z samochodem.W układzie nieinercjalnym związanym z samochodem sytuację widzimy jakby od środka (np. jako sam samochód). W tym układzie samochód i kierowca mają prędkość równą zero; przyspieszenie wypadkowe też wynosi zero (w końcu samochód nie porusza się względem jego kierowcy). |
|||||||||
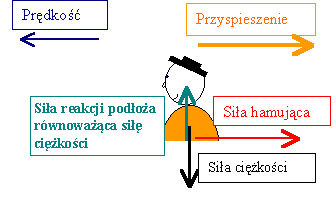
Teraz mamy aż 4 siły działające na kierowcę – 3 siły
wymienione poprzednio i jedna nowa – siła bezwładności:
|
|
||||||||
|
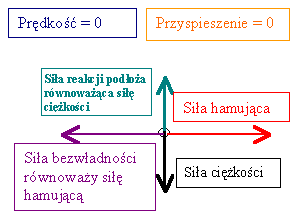
Narysuję te siły jeszcze raz, sprowadzając ludzika do punktu.
W układzie nieinercjalnym wszystkie działające siły równoważą się. W szczególności siła bezwładności równoważy siłę hamującą. Mimo tego, że siły są inne niż poprzednio, to II
zasada dynamiki dalej jest spełniona – bo wypadkowa siła jest równa
zero, ale także przyspieszenie w układzie obserwatora jest równe zero.
Czyli równanie II zasady dynamiki (
|
|||||||||
|
|
|||||||||
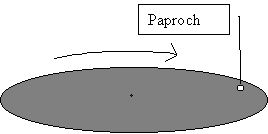
Sytuacja 2 – paproch leżący na brzegu obracającej się płyty gramofonowej |
|||||||||
|
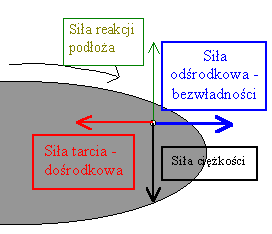
Mamy następującą sytuację – talerz płyty gramofonowej obraca się ze stałą prędkością. Gdzieś blisko krawędzi tej płyty leży sobie paproch. Zastanowimy się znowu nad tym jakie siły na niego działają i jakie z tego wyniknie przyspieszenie?
|
|
||||||||
|
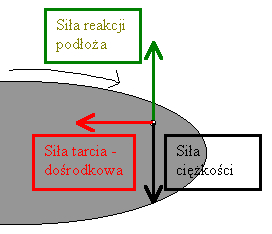
Ponieważ paproch porusza się po okręgu, to musi istnieć siła wypadkowa zakrzywiająca jego ruch, skierowana do środka okręgu (siła dośrodkowa). Źródłem tej siły jest tarcie paprocha o powierzchnię płyty. Dodatkowo na paproch działa oczywiście siła ciężkości dociskająca go do płyty, oraz równoważąca ją siła reakcji podłoża. Siły działające na paproch w układzie inercjalnym |
|||||||||
W układzie inercjalnym patrzymy na paproch i płytę z zewnątrz.
Widzimy tu 3 wymienione wyżej siły:
|
|
||||||||
| Obliczenie siły wypadkowej jest tu proste
– siła reakcji podłoża równoważy tu siłę ciężkości (siły te
znoszą się) i w efekcie zostaje tylko siła dośrodkowa, stając się
jednocześnie siłą wypadkową.
II zasada dynamiki jest tu spełniona, bo różna od zera siła wypadkowa powoduje różne od zera przyspieszenie dośrodkowe. Siły działające na paproch widziane z poziomu układu nieinercjalnegoW układzie nieinercjalnym związanym z samą płytą (lub np. innym paprochem leżącym na tej płycie), oprócz 3 sił opisanych dla układu inercjalnego działa dodatkowo siła bezwładności będąca tu siłą odśrodkową. |
|||||||||
W układzie nieinercjalnym mamy następujące siły:
|
|
||||||||
| Teraz, dzięki dodaniu siły bezwładności,
wszystkie siły się równoważą, a siła wypadkowa staje się równa zero.
II zasada dynamiki (
|
|||||||||
Inne rodzaje sił bezwładnościOprócz wyżej opisanych - czyli siły odśrodkowej, i sił występujących podczas hamowania i ruszania pojazdu, występują pewne bardziej skomplikowane rodzaje sił bezwładności. Najbardziej znaną jest siła Coriolisa. Siła Coriolisa pojawia się wtedy, gdy w obracającym się układzie
nieinercjalnym ciało porusza się ruchem jednostajnym (względem tego układu,
a najczęściej również względem układu inercjalnego). Siła Coriolisa powoduje, że rzeki płynące na północ mają tendencje do podmywania przeciwnych brzegów, niż te płynące na południe. Oczywiście siła bezwładności może mieć swoje bardziej skomplikowane wydania - wszystko zależy od rodzaju ruchu ciała i ruchu układu odniesienia. |
|||||||||
Siła bezwładności – podsumowanie.Siła bezwładności pojawia się zawsze, gdy przechodzimy z opisem do układu nieinercjalnego. Jest ona efektem ruchu samego układu odniesienia i, w odróżnieniu od pozostałych sił, nie wynika z jakiegoś nowego oddziaływania. Siła bezwładności dołączona do równania II zasady dynamiki powoduje zmianę opisu sytuacji – o ile w układzie inercjalnym ciało widziane było jako pozostające w ruchu, to w układzie nieinercjalnym będzie ono w spoczynku (możliwa jest również sytuacja odwrotna, jednak wtedy posługiwanie się układem nieinercjalnym jest mało celowe, ponieważ opis zamiast stawać się prostszym – komplikuje się). Posługiwanie się układami nieinercjalnymi ma sens wtedy, gdy ruch ciał trzeba odnieść do obiektów będących w ruchu przyspieszonym – np. względem obracającej się Ziemi, względem karuzeli, czy pojazdu poruszającego się z przyspieszeniem.
|
|||||||||
|
Powrót na górę strony |
|||||||||