 Druga zasada dynamiki Newtona Druga zasada dynamiki Newtona
Treść drugiej zasady dynamiki brzmi:
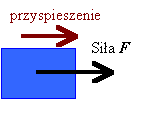
Przyspieszenie jakie
nadaje niezrównoważona siła F ciału o masie m jest
wprost proporcjonalne do tej siły, a odwrotnie proporcjonalne do masy ciała.

Ponieważ zarówno przyspieszenie jak i prędkość są
wielkościami wektorowymi, to precyzyjniej byłoby przedstawić
II zasadę dynamiki w postaci wzoru ze strzałkami nad symbolem siły
i symbolem przyspieszenia.
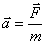
Ta postać wzoru na II zasadę dynamiki mówi nam, nie
tylko o samej wartości przyspieszenia, ale też o kierunku i zwrocie:
Kierunek i zwrot wektora przyspieszenia jest taki sam jak kierunek
i zwrot wektora siły.
Prosty przykład:

Jeśli na ciało o masie 5 kg zadziała niezrównoważona
siła o wartości 2 niutonów, to wartość przyspieszenia tego ciała wyniesie:
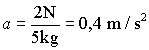
Kierunek i zwrot przyspieszenia ciała będzie zgodny z
kierunkiem i zwrotem działającej siły.
Siła w II zasadzie dynamiki
Jeśli na ciało działa tylko jedna siła, to II zasada
dynamiki jest prosta do zastosowania. Jednak jeżeli sił będzie większa ilość?
- w, 3 albo nawet jeszcze więcej?
- Którą z tych sił podstawić?
Odpowiedź jest prosta. W takiej sytuacji podstawiamy do
wzoru siłę wypadkową. Siła wypadkowa "zawiera w
sobie" wszystkie działające siły składowe i pozwala na poprawne
obliczenie przyspieszenia.
Można więc sformułować II zasadę dynamiki w
postaci.
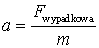
Czy II zasada dynamiki zawsze obowiązuje?
W podstawowej formie II zasada dynamiki Newtona obowiązuje
tylko w układach
inercjalnych. W układach nieinercjalnych pojawia się dodatkowe
przyspieszenie (wynikające z przyspieszenia obserwatora - układu odniesienia),
które "burzy" to równanie.
Jednak da się "uratować" II zasadę dynamiki również
dla układów nieinercjalnych. W tym przypadku jednak do równania trzeba
wprowadzić poprawkę związaną z siłami
bezwładności.
II zasada definiuje siłę
Drugą zasadę dynamiki można właściwie traktować też
jako sposób na zdefiniowanie siły. Wystarczy po prostu zastosować
to równanie dla konkretnego jednego oddziaływania. Więcej informacji na ten temat znajduje się
w rozdziale Definicja
siły.
Uwaga:
Pełne zrozumienie II zasady dynamiki wymaga zapoznania
się także z I
zasadą dynamiki
|