|
|
Układ kartezjański, a inne układy odniesieniaSpis treści rozdziału W celu opisywania położeń ciał w układzie odniesienia stosuje się
różne układy współrzędnych. Najczęściej stosowanym jest kartezjański
układ współrzędnych XYZ. Układ kartezjański na płaszczyźnie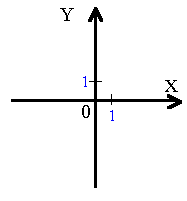 Na płaszczyźnie układ kartezjański stanowią
dwie prostopadle ustawione osie X i Y (lub też określanych jako OX i
OY). Punkt przecięcia tych osi
wyznacza zero układu współrzędnych. Na płaszczyźnie układ kartezjański stanowią
dwie prostopadle ustawione osie X i Y (lub też określanych jako OX i
OY). Punkt przecięcia tych osi
wyznacza zero układu współrzędnych.Aby układ był w pełni zdefiniowany należy na obu osiach zaznaczyć wartości jednostkowe. Oś X nazywana jest osią odciętych, podczas gdy oś Y, to oś rzędnych. Ćwiartki układu współrzędnych |
||||||||
|
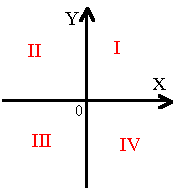
Układ XY dzieli całą płaszczyznę na cztery ćwiartki numerowane przeciwnie do ruchu wskazówek zegara:
|
|
||||||||
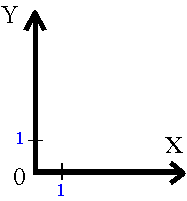
| Gdy opisywana sytuacja mieści się w pierwszej ćwiartce tego układu, stosowany jest uproszczony rysunek obejmujący tylko interesujące nas obiekty i osi zaczynające się od zera. |
|
||||||||
|
P
Aby znaleźć wartości tych współrzędnych należy zrzutować (prostopadle) punkty na odpowiednie osie.
|
|||||||||
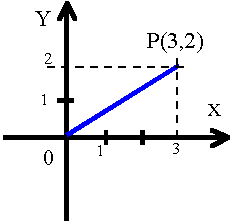 Np.
zapis. P(3,2) oznacza, że Np.
zapis. P(3,2) oznacza, że współrzędna x-owa punktu ma wartość 3, a y-owa ma wartość 2. |
|||||||||
Układ kartezjański w przestrzeni
|
|||||||||
|
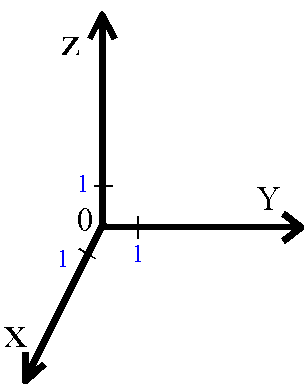
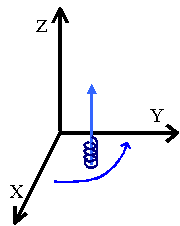
Układ trzech współrzędnych kartezjańskich XYZ rysujemy w sposób prawoskrętny (posługując się regułą śruby prawoskrętnej). Oznacza to, że zwrot osi Y jest zależny od nazwania osi X i Z. Gdybyśmy wkręcali śrubę (prawoskrętną, czyli taką jak wszystkie typowe śruby w Polsce) w kierunku od osi X do osi Y, to śruba ta powinna posuwać się (wkręcać) wskazując zwrot osi Z.
|
|
||||||||
|
Położenie punktu w przestrzeni w układzie kartezjańskim podaje się za pomocą trzech liczb X,Y,Z - współrzędnych x-owej, y-owej i z-wej. Np. P(1,3,2) oznacza, że współrzędne
|
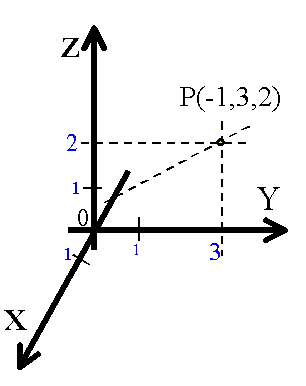
|
||||||||
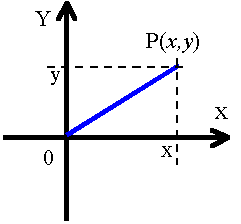 ołożenie punktu na płaszczyźnie w układzie
kartezjańskim podaje się za pomocą dwóch liczb współrzędnych:
ołożenie punktu na płaszczyźnie w układzie
kartezjańskim podaje się za pomocą dwóch liczb współrzędnych: