|
|
|||||||||||||||||||
|
|
Cykl
Carnota - wstęp
|
||||||||||||||||||
|
omawia się cykle termodynamiczne, | |
|
przedstawia cykl Carnota, | |
|
a następnie podaje II zasadę termodynamiki. |
Ten schemat nauczania sugeruje, że pokazanie związku między cyklem Carnota, a II zasadą dynamiki, wydaje się być „wyższą” wiedzą, zarezerwowaną wyłącznie dla ekspertów. Jednak nie jest to prawda, ponieważ można w stosunkowo nieskomplikowany sposób pokazać dlaczego cykl Carnota jest cyklem od największej możliwej sprawności. Później dość łatwo można stąd uzasadnić II zasadę termodynamiki. Dodatkową zaletą opisywanej metody jest przećwiczenie umiejętności interpretacji wykresów oraz intuicyjna graficzna forma.
Rozumowania przedstawionego poniżej nie spotkałem nigdzie w literaturze (co oczywiście nie znaczy, że go nie ma), więc to opracowanie może być sporą pomocą w nauczaniu termodynamiki w liceach ogólnokształcących. Być może jest ono zbyt skomplikowane dla przeciętnego ucznia, lecz na pewno jest do zaakceptowania na poziomie fakultetu fizycznego lub w klasach profilowanych matematycznie.
Problem podstawowy - założenia
Rozważmy więc podstawowy dla naszego zagadnienia problem:
Jak powinien przebiegać cykl termodynamiczny o teoretycznie największej sprawności?
Aby nasze rozważania na czymś oprzeć przyjmiemy pewne dodatkowe założenia:
|
substancją roboczą jest gaz doskonały | |
|
mamy silnik cieplny w postaci
naczynia, w którym możemy zmieniać temperaturę i objętość gazu
- a więc cylinder z tłokiem. | |
|
poprzez ścianki cylindra możemy dostarczać i odbierać ciepło, zaś dzięki ruchowi tłoka możemy pobierać i dostarczać pracę | |
|
substancja robocza pracuje w cyklu zamkniętym, a poszczególne przemiany są kwazistatyczne, czyli odwracalne | |
|
dysponujemy pewną skończoną ilością ciepła Qp , którą możemy dostarczyć w jednym cyklu pracy silnika | |
|
temperatura substancji roboczej nie może przekroczyć zakresu pewnych ustalonych wartości: |
Przyjmiemy oznaczenia:
T1- temperatura grzejnika - maksymalna możliwa temperatura, a jednocześnie temperatura ciała ogrzewającego nasz gaz zachodzi taka potrzeba
T2 - temperatura chłodnicy - minimalna możliwa temperatura, a jednocześnie temperatura ciała odbierającego ciepło jeśli zajdzie taka potrzeba.
Zakres temperatur
Teraz postaram się problem zobrazować na wykresach co bardzo pomaga w zrozumieniu. Zacznijmy założenia dotyczącego temperatur. Przyjęty ich zakres da się zobrazować na wykresie w układzie pV (ryc. 1)
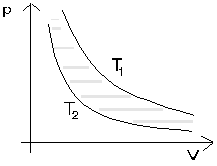 ryc.1
ryc.1
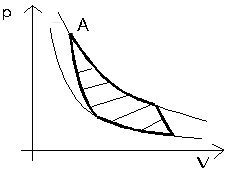
Hiperbole na tym wykresie to oczywiście izotermy odpowiadające minimalnej i maksymalnej temperaturze.
Obszar na wykresie pomiędzy tymi izotermami, jest obszarem dozwolonych stanów naszego idealnego silnika cieplnego. Wykroczenie poza ten obszar oznaczałoby przekroczenie założonego zakresu temperatur.
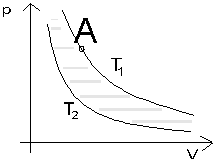
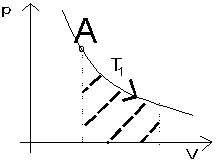
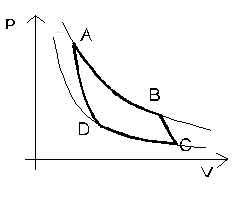 Ryc. 5
Ryc. 5