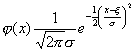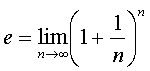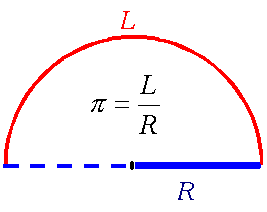
Interpretacja liczby π 

Liczba π  (pi) jest wartością stosunku łuku półokręgu, do promienia tego półokręgu. 

Liczba π jest liczbą przestępną - tzn. posiada nieskończoną liczbę cyfr rozwinięcia dziesiętnego (podane cyfry to tylko pierwsze z tego nieskończonego szeregu).

Niektóre wzory zawierające liczbę π.

Pole koła

P_o = π R²

Obwód okręgu (koła)

L = 2 π R

Funkcja Gaussa na rozkład normalny:

Interpretacja liczby e

Liczba e  dana jest wzorem:

Liczba "e" też jest liczbą przestępną, a więc ma nieskończoną liczbę cyfr rozwinięcia dziesiętnego.

Liczba e jest ściśle powiązana z logarytmem naturalnym i słuszne są wzory:

ln e = 1

Logarytm naturalny jest to szczególny logarytm, ponieważ wyznacza on funkcję niezwykle ważną w rachunku różniczkowym i całkowym = funkcję e^x zwaną także funkcją exp(x)

Funkcja

y(x) = e^x

jest szczególna ponieważ jako jedyna ze wszystkich funkcji różnowartościowych jest równa swojej pochodnej (i to pochodnej dowolnego rzędu).

,

Poza tym logarytm naturalny jest funkcją bardzo ważną z tego powodu, że jego pochodna ma wartość 1/x, zaś całka nieoznaczona z funkcji 1/x, równa jest ln e.