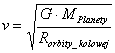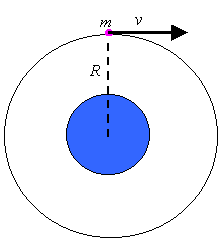
Grawitacja

Teoria

Wprowadzenie

Wzór Newtona na siłę grawitacji

Przykład zastosowania wzoru

Wektorowa postać wzoru

Orbity kołowe
I prędkość kosmiczna

Orbity eliptyczne

Stan nieważkości

Czytanki

O grawitacji słów kilka

Grawitacja, a filozofia

(Roz)działy powiązane

Ciężar ciała

Masa

Teoria względności

W przygotowaniu
II prędkość kosmiczna
Praca w polu grawitacyjnym
Prawa Keplera
Ważne zadania i problemy

Prędkość ruchu satelity na orbicie kołowej

Zastanówmy się teraz nad pytaniem:
Jakiej prędkości ciała potrzeba, aby ciało utrzymywało się na orbicie kołowej w odległości R od środka planety?

Odpowiedź na to pytanie będzie wymagała zastosowania wzoru na siłę grawitacji.
Aby mieć jasność co jest tu dane, a czego szukamy, założymy że:
- W odległości R od środka planety krąży ciało o masie m. 
- Prędkość tego ciała jest skierowana prostopadle w stosunku do promienia i wynosi v. 
- Masę planety oznaczymy przez M.

Wyjaśnienia

Dla rozwiązania naszego problemu musimy uświadomić sobie jaką rolę pełni grawitacja w stosunku do ruchu ciała.
- Odpowiedź na to pytanie nie jest trudna: grawitacja, ciągnąc ciało w kierunku środka planety, zakrzywia ten ruch nadając mu kształt okręgu.

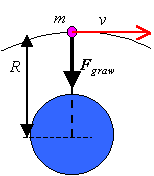
Jak wielka jest wartość siły zakrzywiającej?

Ale żeby to zakrzywienie miało dokładnie kształt okręgu, wartość siły grawitacji musi zrównać się z siłą dośrodkową potrzebną do utrzymania ciała na orbicie:

F_graw = F_dośr

A ponieważ siła grawitacji dana jest znanym wzorem  (prawo grawitacji powszechnej Newtona):

Podstawimy tu oznaczenia wartości wg ustaleń z początku rozdziału:

    
(m masa ciała orbitującego, M – masa planety, R – promień orbity)

Skorzystamy także ze wzoru na siłę dośrodkową – patrz Siła dośrodkowa,  tablice wzorów (v - prędkość),

więc, po podstawieniu obu wartości sił do równania F_graw = F_dośr, otrzymamy

A stąd po pomnożeniu obu stron przez R/m, po obu stronach skróci się R i m, i dostaniemy:

Teraz zamienimy strony równania i spierwiastkujemy je:

Powyższy wzór pozwala na obliczenie prędkości jaka musi mieć ciało, aby orbitowało wokół planety dokładnie po orbicie kołowej o promieniu R.

Zapiszemy go jeszcze raz dokładnie określając o jakie wielkości chodzi:

I to jest właśnie nasz szukany wzór na prędkość ruchu satelity na orbicie kołowej. Wzór ten służy do obliczania tzw. pierwszej prędkości kosmicznej. 

Orbity kołowe > I prędkość kosmiczna

Orbity eliptyczne