Jak to zrozumieć i pokazać "machając rękami"?

Słowo „zrozumieć” oznacza najczęściej wytworzenie sobie w umyśle określonego obrazu, który ilustruje mechanizm działania jakiegoś prawa. Rzeczywistość akademicka nie przejmuje się tym wyobrażeniem rozumienia – fizycy, gdy chcą coś wykazać, wyciągają kredę a następnie maczkiem zapisują kilkanaście stron tekstu matematycznego najeżonego całkami, logarytmami i innymi atrakcjami z analitycznego piekła rodem. Z kolei dla mnie (a chyba nie tylko dla mnie) najlepszym sposobem pokazania czegoś jest przekonanie delikwenta bez wzorów – najlepiej za pomocą prostych słów i gestów, a w fizyce – paru narysowanych obrazków. Powyższą metodę tłumaczenia umownie określam jako „metodę machania rękami”.

Niniejszym więc, na przykładzie prostych rozważań geometrycznych, postaram się wyjaśnić dlaczego z pewnych prostych założeń wynika, że czas w układzie poruszającym się musi płynąć wolniej oraz, że długości ulegają skróceniu w kierunku ruchu.

Dylatacja czasu

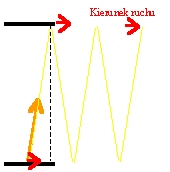
Przykład poniższy zaczerpnąłem z podręcznika do fizyki dla liceum P. dra Kozielskiego, przedstawię go jednak w sposób osobisty – tzn. nie zaglądając do tekstu pomysłodawcy (nie dysponuję tą książką w swoich zbiorach bibliotecznych), opierając się na pamięci i dodając trochę fantazji.

Zastanówmy się jak w istocie mierzymy czas. Przypomnienie sobie zasad działania większości zegarów pokazuje, że najczęściej pomiar ten jest oparty o jakieś jednostajnie zachodzące zjawisko. Pierwszymi zegarami były klepsydry przesypujące piasek lub przelewającymi wodę, później wahadła, a dopiero ostatnio owym ruchomym medium stały się drgania elektryczne w zegarkach kwarcowych.

My, bardziej tradycyjnie, posłużymy się klepsydrą. Jednak będzie to klepsydra unowocześniona – klepsydra świetlna, w której elementem „ruchomym” jest światło.

Wyobraźmy sobie, że mamy dwa idealnie odbijające zwierciadła, które uwięziły promień światła odbijający się między nimi. Dzięki prostopadłemu zwierciadeł względem ruchu promienia, będziemy mogli mierzyć czas – narasta on wraz z ilością odbić promienia świetlnego, czyli „odwróceń” naszej klepsydry. Np. jeśli odległość między zwierciadłami wynosi 3 m, to czas upływający pomiędzy odbiciami wynosi jedną setną mikrosekundy (prędkość światła to 300 mln. m/s, a więc na przebycie trzech metrów światło potrzebuje właśnie jedną stumilionową sekundy). Mierząc ilość odbić światła od zwierciadeł będziemy mogli precyzyjnie ustalić upływ czasu - np. milion odbić, będzie wyznaczało czas 1/100 s.

Zaletą tego zegara jest zastosowanie światła, którego prędkość jest stała we wszystkich układach odniesienia. Dlatego łatwo będzie nam porównywać wskazania tego zegara dla różnych obserwatorów.

Klepsydra w ruchu

Zastanówmy się teraz jakie będą wskazania naszej klepsydry świetlnej, jeśli będziemy obserwować ją w ruchu. Zegar ustawimy prostopadle do kierunku ruchu, aby nie przeszkadzało nam dodatkowo ew. skrócenie długości jakie występuje dla ustawienia zgodnego prędkością.

Z rysunku widać, że światło obserwowane w ruchu przebywa nie tylko drogę prostopadle do drogi pomiędzy zwierciadłami, ale uzyskuje także składową wzdłuż kierunku ruchu. Obrazowo mówiąc: bieg promieni rozciąga nam się jak harmonia, ponieważ kolejne punkty, które odwiedza światło przesuwają się dla obserwatora ruchomego. Dlatego ostatecznie musi ono przebyć nieco dłuższą drogę niż dla zegara spoczywającego – przecież teraz porusza się po przekątnej prostokąta w którym zawiera się obraz jednego odbicia promienia. Ale przebycie dłuższej drogi przy tej samej prędkości (przypominam, że wartość prędkości światła jest stała we wszystkich układach odniesienia), oznacza dłuższy czas jej przebywania. Dlatego czas pomiędzy poszczególnymi odbiciami promienia jest dłuższy w układzie poruszającym się niż spoczywającym.

Patrz także - wytłumaczenie skrócenia długości