Skrócenie długości - wytłumaczenie w oparciu o rozważania geometryczne

Teoria względności
dla psychologów

Jak to funkcjonuje?

Dylatacja czasu

Skrócenie długości

Inne, powiązane

Wzory teorii względności

Rozważania o tw

Zik - opowiadanie fantastyczne

Jeszcze jedna wątpliwość

Uzupełniające

Układy odniesienia - definicja ogólna

Czym jest światło?

Skrócenie długości - tłumaczenie skrótowe

Skrócenie długości w pewnym stopniu częściowo wynika z faktu spowolnienia czasu. Jeśli gdzieś odległość między punktami będziemy mierzyć czasem lotu promienia świetlnego, to krótszy czas lotu, w innym układzie odniesienia, automatycznie będzie odpowiadał mniejszej odległości.

Jednak dlaczego skrócenie długości występuje tylko dla kierunku zgodnego z kierunkiem ruchu? – przecież światło rozchodzi się z jednakową prędkością w każdą stronę... Czyżby czas miał „kierunek” i był inny dla promieni równoległych, a inny dla prostopadłych względem prędkości obiektu?
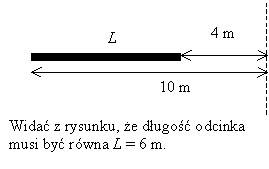
Wyjaśnienie tych problemów nie jest proste, dlatego postaram się przedstawić bardziej "porządne" rozumowanie, oparte o rozważania geometryczne. Wytłumaczenie to jest nieco skomplikowane, a chociaż nie operuje wzorami i wymagane umiejętności matematyczne sprowadzają się do zrozumienia zasady dodawania długości odcinków, to trzeba trochę nad nim "przysiąść".
Kto się nie boi – niech czyta następujący niżej rozdział.

Skrócenie długości - dokładne wytłumaczenie w oparciu o myślowe doświadczenie.

Precyzyjne okazanie zjawiska skrócenia długości w układzie poruszającym się jest bardziej skomplikowane, niż to ma miejsce w przypadku dylatacji czasu.

Najpierw ustalmy na czym polega pomiar długości. Sprawa jest o tyle skomplikowana, że dla bardzo szybko poruszających się obiektów nie sposób jest przyłożyć miarki aby odczytać ile dany odcinek ma metrów, czy centymetrów. Trzeba więc posłużyć się inną metodą. Einstein zaproponował tu wykorzystanie światła (wciąż to światło...). Jeżeli obiekt spoczywa, to po prostu wyznaczamy czasy w jakich promień świetlny leci do nas od jednego i drugiego końca odcinka. Gdy odcinek się porusza, to złapanie promienia nie jest też takie proste – przecież cały czas początek i koniec mierzonego odcinka zmieniają położenie i nie bardzo wiadomo, które punkty ze sobą porównywać.

Zajmijmy się jednak najpierw tym prostszym przypadkiem. Wiadomo jeśli w linii prostej do początku odcinka jest 4m, a do końca 10m to długość odcinka będzie równa 6m.

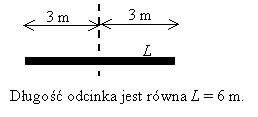
Można też wyznaczać odległości od końców odcinka mierząc odległości od środka odcinka:

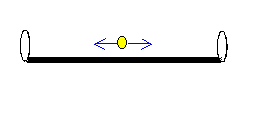
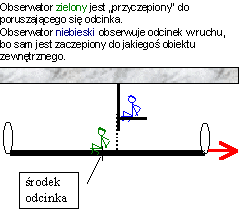
W przypadku odcinka w ruchu, wyznaczanie odległości jest trudniejsze, bo zarówno początek, jak i koniec odcinka bez przerwy się nam przesuwają. Dlatego niezwykle ważne jest, aby przypilnować tego, że położenia początku i końca trzeba wyznaczyć w tym samym czasie. Bo odległość między poruszającymi się punktami, wyznaczana w różnych momentach nie da nam na pewno dobrej długości odcinka.

Aby więc zagwarantować, określanie końców odcinka w tym samym czasie proponuję użycie następującej metody:

Do końców mierzonego odcinka przyczepimy zwierciadła.

	Do tych zwierciadeł będziemy wysyłać promienie świetlne. Mierząc czas, po którym odbity promień wróci, będziemy mogli wyznaczyć odległość zwierciadła w momencie odbicia
	Promienie świetlne będziemy wysyłać gdzieś z punktu położonego między zwierciadłami - tam będzie źródło sygnału radarowego sprzężone z detektorem, czyli z odbiornikiem promieni. Detektor będzie oczywiście wyposażony w zegar umożliwiający określenie czas lotu promieni świetlnych.

Aby zagwarantować, że odbicie od obu końców zajdzie jednocześnie, można postąpić tak: co niewielki ułamek sekundy wysyłane są promienie świetlne w obie strony. Każdy wysłany promień światła różni się minimalnie kolorem od poprzedniego. Później, gdy będziemy analizować światło odbite weźmiemy pod uwagę tylko te promienie, które wrócą jednocześnie i będą miały ten sam kolor (aby nie było sytuacji, w której od odebraliśmy jeden promień odbity od zwierciadła wcześniej, a drugi później, co jest możliwe gdyby punkty odbicia były w różnych odległościach od detektora). Zmierzony czas, po którym wysłane promienie wrócą po odbiciu będzie miernikiem długości odcinka – ponieważ każdy promień pokonuje swoją połówkę odcinka 2 razy to znaczy, że wystarczy wymnożyć czas lotu dowolnego z dwóch promieni przez prędkość światła, aby dostać szukaną długość odcinka.

Wyobraźmy sobie teraz, że nasz długość naszego odcinka będzie mierzona w dwóch różnych układach odniesienia:

	Pierwszy układ odniesienia, to układ na sztywno związany z odcinkiem. Odcinek w nim spoczywa.
	Drugi układ odniesienia jest w ruchu względem odcinka, czy (co na to samo wychodzi) odcinek jest w ruchu względem niego

Uwaga: na tym, i następnych rysunkach, mierniczego związanego z układem spoczywającym względem odcinka będę oznaczał kolorem zielonym, a mierniczego obserwującego odcinek w ruchu – niebieskim.

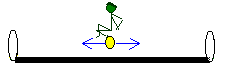
Rozważmy teraz jak będzie zachodził pomiar długości w tych układach odniesienia.

1 układ, w którym odcinek spoczywa (zielony)

Tutaj sytuacja jest bardzo prosta – skoro nasz miernik odległości cały czas znajduje się dokładnie w środku odcinka, to promienie odbite będą miały identyczną drogę do przebycia i będą wracały jednocześnie.

Czas powrotu wysłanych promieni pomnożony przez prędkość światła da nam długość odcinka. Nie ma znaczenia, w którym momencie te promienie będą wysłane – byle tylko zawsze startowały ze środka odcinka - i tak wszystkie wysłane promienie tego samego koloru będą wracać jednocześnie.

Oczywiście inaczej byłoby, gdyby nasz miernik znajdował się nie w środku odcinka, dlatego można powiedzieć, że fakt jednoczesnego przyjścia promieni odbitych jest jednocześnie wskaźnikiem ustawienia detektora w środku.

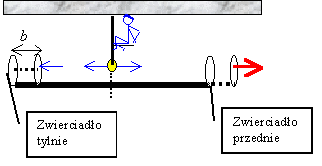
2. pomiar odległości odcinka poruszającego się (dla obserwatora niebieskiego)

Tutaj sytuacja jest znacznie bardziej skomplikowana. Dla obserwatora próbującego zmierzyć odcinek w ruchu, zwierciadła odbijające cały czas zmieniają swoje położenie. Przypadkowo wysłane promienie świetlne zapewne odbiją się od zwierciadeł w różnym czasie i dlatego nie dadzą nam informacji o długości odcinka.

Np. gdybyśmy próbowali dokonać pomiaru wysyłając promień w chwili, gdy mija nas dokładnie środek odcinka, to jedno zwierciadło (na rysunku lewe) zdążyłoby się do momentu odbicia nieco przybliżyć do detektora (na rysunku o odcinek b). Drugie zwierciadło (prawe) miałoby za to czas, aby się oddalić. W efekcie promienie odbite nie wróciłyby jednocześnie do detektora, a my mielibyśmy odczyty położeń zwierciadeł dokonane w różnym czasie.

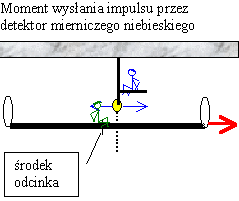
Dlatego aby zagwarantować, że odbicia od zwierciadeł będą następować w tym samym czasie, musimy zacząć wysyłać impulsy świetlne szybko jeden po drugim. Jeśli zaczniemy tak robić zaraz po tym jak detektor minie pierwszy koniec odcinka, to najpierw będą przychodzić impulsy odbite właśnie od przedniego zwierciadła (które oddala się od detektora), a dopiero po znacznie dłuższym czasie od zwierciadła tylnego. Jednak wraz z przesuwaniem się zwierciadeł czasy przylotu promieni będą się stawać coraz bliższe sobie – pierwsze zwierciadło będzie się od detektora oddalać, a drugie przybliżać. W pewnym momencie jeden z tych czasów spełni nasz warunek jednoczesnego przyjścia obu wysłanych promieni (zakładamy, że impulsy świetlne są wysyłane rzeczywiście bardzo często jeden po drugim) – i o ten właśnie przypadek nam chodzi. Zauważmy, że ów interesujący nas promień odbija się od obu zwierciadeł dokładnie w momencie, w którym środek odcinka mija obserwatora.

Następne impulsy będą oczywiście przychodziły rozsynchronizowane, bo przednie zwierciadło oddali się już dalej niż tylnie.

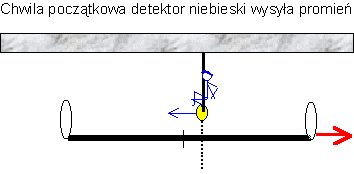
Zastanówmy się teraz nad sytuacją w dojdzie do naszego właściwego pomiaru – tzn. gdy promienie wysłane do obu zwierciadeł jednocześnie wrócą do detektora. Wysłanie owego kluczowego impulsu powinno nastąpić nieco przed momentem, w którym środek odcinka wraz z mierniczym zielonym mija detektor niebieski.

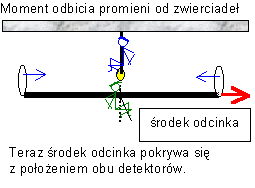
Dzięki temu, podczas lotu promienia zwierciadła przesunie się na tyle, że samo odbicie od nich nastąpi dokładnie w chwili, gdy środek odcinka i oba detektory znajdą się tym samym punkcie.

W tym samym momencie, gdy promienie będą jednocześnie odbijane od zwierciadeł, oba detektory znajdują się w jednym punkcie. Wtedy impulsy trafią parami jednocześnie do detektora, a czas ich lotu będzie miarą długości odcinka.

Powiązanie ze sobą pomiarów zachodzących w obu układach

Teraz najtrudniejszy moment – musimy powiązać ze sobą odczyty czasów lotu promieni (a więc i długości odcinków) następujące w układzie, w którym odcinek porusza się (niebieskim) i w układzie względem odcinka nieruchomym (zielonym).

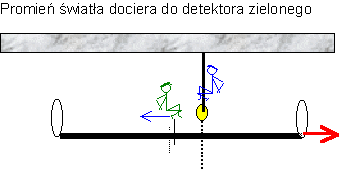
W tym celu przyjrzyjmy się co dzieje się z impulsem świetlnym wysłanym przez detektor niebieski. W czasie lotu do zwierciadła tylnego, w pewnym momencie, mija on środek odcinka (a więc także znajdujący się tam detektor zielony).

Zwróćmy uwagę na jedną rzecz: lecący promień od detektora niebieskiego może służyć mierniczemu zielonemu „jak własny” – wystarczy tylko, że w momencie mijania go omawianego promienia dodatkowo wyśle bliźniaczy promień w przeciwnym kierunku do zwierciadła przedniego. Wtedy całość będzie mógł uznać także za swój pomiar długości. Tak więc od momentu minięcia środka odcinka przez lecący promień, pomiar czasu (a zatem i odległości) będzie dla obu mierniczych wspólny.

Cóż się dalej więc z owym wspólnym pomiarem dzieje?

	najpierw impuls świetlny dolatuje do zwierciadła i oczywiście natychmiast odbija się od tegoż zwierciadła (w momencie odbicia pokrywają się ze sobą środek odcinka i położenie obu detektorów – tego mierzącego długość odcinka w ruchu i tego spoczywającego)
	impuls leci z powrotem. W tym czasie detektor obserwatora zielonego związanego ze środkiem odcinka przesuwa się już za detektor mierniczego niebieskiego.
	impuls dociera z powrotem do detektora, z którego został wysłany (niebieskiego) – pomiar obserwatora patrzącego na odcinek z zewnętrz zostaje tu zakończony – tutaj więc kończy się wspólna część lotu promieni. Jednak do tej chwili środek odcinka wraz z detektorem zielonym przesunął się na odległość od detektora niebieskiego równą tej, w której znajdował się podczas startu impulsu (tyko teraz jest po przeciwnej stronie). Załóżmy więc, że detektor niebieski nie pochłonie całej wiązki światła (np. jest ona szeroka), jej część przelatuje swobodnie obok zmierza teraz do detektora zielonego, aby zostać tam zarejestrowana.

Na koniec impuls dociera do zielonego detektora.

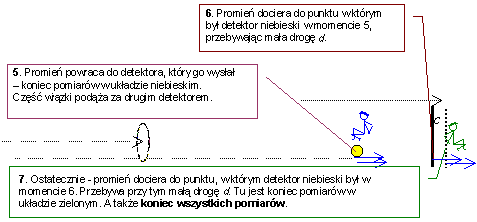
Pojawia się teraz pytanie zasadnicze:

Który z naszych dwóch mierniczych (zielony, czy niebieski) zarejestrował dłuższy czas przelotu sygnału mierniczego?

A może nie było różnicy, między tymi czasami?

Jasne jest, że dłuższy czas odpowiada dłuższej przebytej drodze, a zatem zarejestrowaniu większej wartości długości odcinka.

Aby odpowiedzieć sobie na to pytanie. Trzeba prześledzić lot promieni bardzo dokładnie, bo istnieje dość subtelna różnica między zmierzonymi czasami przelotu.

Porównajmy jednak najpierw główne czasy przelotu promieni. W tym celu podzielimy wszystkie etapy ruchu na rozłączne odcinki (patrz rysunek). Aby wyjaśnienia były czytelne drogę promienia jest rozbita na dwa rysunki. Kolejność następujących zdarzeń wynika z numeracji opisów – od 1 do 7.

Teraz promień świetlny udaje się w drogę powrotną

Zastanowimy się teraz dla którego z układów promień mierniczy przebył dłuższą drogę.

Najpierw rozpiszemy drogę dla układu niebieskiego. Składa się ona z odcinków:

1 – 2, 2 – 3, 3 – 4, 4 – 5.

Teraz droga dla układu zielonego. Właściwe odcinki to:

2 – 3, 3 – 4, 4 – 5, 5 – 6, 6 – 7.

Widać od razu, że odcinki: 2 – 3, 3 – 4, 4 – 5 pokrywają się. Różnica zawiera się w odcinkach:

1 – 2: występujący tylko dla układu niebieskiego.

5 – 6, 6 – 7: występujące tylko dla układu zielonego.

Myślę, że uważny czytelnik zauważy, że odcinek 1 – 2 jest krótszy od sumy odcinków 5 – 6 i 6 – 7. Mało tego - jest on nawet krótszy od samego odcinka 5 – 6, i to o długość d. Ponieważ zaś dochodzi do tej różnicy jeszcze jedna wartość d (bo tyle wynosi długość odcinka 6 – 7), więc widzimy, że:

droga promienia w układzie zielonym jest dłuższa od drogi w układzie niebieskim o 2d.

A to oznacza, że:
Czas pomiaru odległości w układzie zielonym jest większy niż w układzie niebieskim.

A ponieważ czas świadczy o długości odcinka, więc możemy powiedzieć:

W układzie niebieskim zmierzona długość odcinka jest krótsza!

Uogólniając:
Obserwator mierzący długość odcinka będącego w ruchu uzyska rezultat mniejszy niż obserwator względem tego odcinka spoczywający.

A to jest właśnie owo sławetne relatywistyczne skrócenie długości.

Patrz także -wytłumaczenie dylatacji czasu