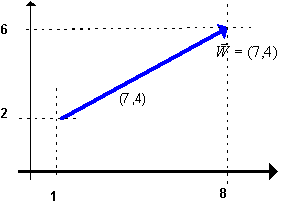|
|
Wektory - ujęcie graficzne i ujęcie
analityczne
Wektory przedstawia się zazwyczaj na dwa
sposoby:
ujęcie graficzne:
uzyskujemy przez narysowanie strzałki na płaszczyźnie lub w
przestrzeni.
ujęcie analityczne:
układ dwóch liczb - współrzędnych (na płaszczyźnie),
lub trzech liczb (w przestrzeni)
|
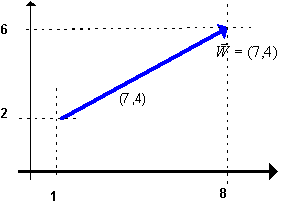
związek między dwoma ujęciami wektora - strzałką wektora (ujęcie
graficzne) i liczbami opisującymi położenie początku i końca strzałki. |
| Współrzędne wektora otrzymujemy odejmując od współrzędnych
końca wektora, współrzędne początku tego wektora. |
 | współrzędna x - owa wektora na rysunku ma wartość 7
(znajdujemy różnicę współrzędnych końca i początku wektora:
8 - 1 = 7). |
 | współrzędna y - owa w naszym wypadku ma wartość 4
(bo 6 - 2 = 4). |
Ostatecznie więc na powyższym rysunku mamy wektor (7,4).
|
Oba ujęcia - graficzne i analityczne - są równoważne, tzn. dają zgodne ze sobą wyniki. Zaletą ujęcia
graficznego jest lepsze działanie na wyobraźnię; zaletą ujęcia
analitycznego jest łatwość obliczeń matematycznych oraz możliwość
tworzenia wektorów o więcej niż trzech wymiarach (znacznie trudniej
byłoby wyobrazić sobie np. sześciowymiarowe wektory jako strzałki).
|