| rodzaj działania |
zapis i typ wielkości wynikowej
|
opis wielkości wynikowej
|
| Dodawanie wektorów |
Żeby dodać dwa wektory, gdy znamy ich współrzędne,
należy dodać odpowiednie współrzędne - x-owe do
x-owych, a y-owe do y-owych (ew. z-owe do z-owych).
Na płaszczyźnie
(wx, wy) + (ux,
uy) =
(wx+ux, wy+uy)
W przestrzeni
(wx, wy,
wz ) + (ux, uy,
uz) =
(wx+ux, wy+uy,
wz + uz) |
W odróżnieniu od dodawania liczb całkowitych
wektor-suma wcale nie musi być dłuższy od któregoś z wektorów
wyjściowych, a często bywa krótszy.
Suma dwóch wektorów może być też wektorem zerowym (mimo, że
wektory wyjściowe miały długości różne od zera)
Zachodzi to w dwóch przypadkach:
- oba sumowane wektory są zerowe
- dodawane wektory są
przeciwne - tzn. mają ten sam kierunek i wartość, ale
przeciwne zwroty.
Patrz także: Dodawanie
graficzne wektorów oraz Dodawanie
algebraiczne wektorów, Siła. |
| Odejmowanie wektorów |
Żeby odjąć dwa wektory, gdy znamy ich współrzędne,
należy odjąć odpowiednie współrzędne - x-owe od
x-owych, a y-owe od y-owych (ew. z-owe od z-owych).
Na płaszczyźnie
(wx, wy)
- (ux, uy) =
(wx - ux, wy
- uy)
W przestrzeni
(wx, wy,
wz ) - (ux, uy,
uz) =
(wx - ux, wy
- uy, wz - uz) |
Wektor-różnica wcale nie musi być krótszy od
pierwszego z wektorów wyjściowych. Może być dłuższy.
Różnica dwóch wektorów jest równa zero (jest wektorem
zerowym) w dwóch przypadkach:
- oba odejmowane wektory są zerowe
- odejmowane wektory są równe - tzn. mają ten sam kierunek,
zwrot i wartość.
Patrz też: Dodawanie
graficzne wektorów oraz
Dodawanie
algebraiczne wektorów. |
| mnożenie
wektora przez liczbę
Tak samo dzielenie przez liczbę.
|
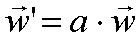
otrzymujemy nowy wektor
Aby wektor podzielić przez liczbę, mnożymy go
przez odwrotność tej liczby
|
powstaje wektor a razy dłuższy od wektora
wyjściowego.
Zwrot wektora wynikowego jest:
- taki sam jak wyjściowy, gdy a jest dodatnie
- przeciwny do wyjściowego, gdy a jest ujemne
Wynik może być równy zero (będzie tzw. wektorem zerowym)
gdy:
- wektor wyjściowy jest równy zero, lub
- liczba a jest równa zero
|
| mnożenie skalarne
wektorów |
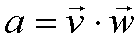
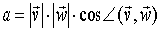
otrzymujemy skalar
|
Powstaje liczba (skalar) o wartości równej
iloczynowi wartości obu wektorów razy kosinus kąta między nimi
zawartego.
Lub inaczej:
Iloczyn skalarny jest równy iloczynowi długości jednego wektora
mnożonego przez długość rzutu drugiego wektora na
kierunek wyznaczony przez pierwszy wektor (skomplikowane jest to
zdanie, ale prościej chyba się nie da...). Dokładniej wyjaśnione
jest to w dziale Energia
przy omawianiu pracy.
Iloczyn skalarny stanie się równy Zero, gdy którykolwiek z
wektorów wyjściowych jest zerowy, lub wektory są do siebie
prostopadłe.
Patrz także: Mnożenie
skalarne wektorów.
|
mnożenie wektorowe
wektorów (stosuje się
wyłącznie do wektorów w trzech
wymiarach)
|
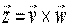
otrzymujemy nowy wektor prostopadły do
obu wektorów wyjściowych.
Długość (wartość) tego wektora
wynosi: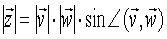
Uwaga:
tak naprawdę efektem mnożenia wektorowego wektorów jest
tensor... Ale w uproszczeniu możemy go traktować jako wektor a właściwie
tzw. "pseudowektor".
|
- wartość wektora wynikowego jest równa
iloczynowi wartości obu wektorów wyjściowych razy sinus kąta
między nimi zawartego (ma to sens tylko w trzech wymiarach);
- kierunek wektora wynikowego jest prostopadły do płaszczyzny
wyznaczonej przez wektory wyjściowe;
- zwrot ustalamy w oparciu o regułę
śruby prawoskrętnej
Interpretacja iloczynu wektorowego 2:
Wartość iloczynu wektorowego jest równa iloczynowi długości
pierwszego wektora przez długość rzutu drugiego wektora na
kierunek prostopadły do pierwszego wektora.
Wektor zerowy otrzymamy, gdy jeden z wektorów wyjściowych
jest zerowy, lub gdy wyjściowe wektory są równoległe.
|
znajdowanie
wartości
(długości) wektora gdy znamy jego współrzędne |
Długość wektora na płaszczyźnie obliczamy
stosując twierdzenie Pitagorasa.
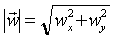
Żeby obliczyć wartość wektora trójwymiarowego
trzeba zastosować to twierdzenie dwa razy.
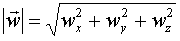
|
Długość wektora jest równa zero tylko wtedy, gdy wszystkie
współrzędne wektora są równe zero (ew. patrz wektor
zerowy).
Jeśli wektor podany jest w postaci rysunkowej, to trzeba
zmierzyć długość strzałki tego wektora, a następnie pomnożyć
przez skalę w jakiej został narysowany - np. jeśli centymetr
oznacza 3 m/s, to wektor 5 centymetrowy oznacza prędkość o
wartości 15 m/s.
Patrz także: Wartość wektora
|