Wektory jednowymiarowe i umowa znaku osi

Szczególnym przypadkiem wielkości, która jest czymś pośrednim między wektorem, a skalarem, jest wektor jednowymiarowy (który można by też uznać za skalar). Co prawda, jak to wyżej napisano skalary są najczęściej wielkościami nieujemnymi, jednak nie jest to ściśle przestrzegana reguła.

W każdym razie można tu przyjąć, że wektor jednowymiarowy, to liczba ze znakiem (może więc być dodatnia, lub ujemna).
Wektor jednowymiarowy, jest to wielkość w fizyce bardzo ważna, bo będąc formalnie wektorem (a przynajmniej wywodząc się ściśle od wektorów), nie posiada wad formalizmu wektorowego (kłopotliwości rachunkowych, wielu wymiarów do przekształcania). Dlatego wektory te są często wykorzystywane.
W przypadku wektora jednowymiarowego rolę zwrotu przejmuje znak liczby. Kierunek nie jest w tym przypadku istotny, bo i tak wszystko dzieje się w jednym wymiarze, więc jest on z góry określony.
Za pomocą wektorów jednowymiarowych opisuje się takie wielkości jak:

	prędkość w ruchu prostoliniowym (lub w ruchu po ściśle określonym torze)
	przyspieszenie w ruchu prostoliniowym (lub w ruchu po ściśle określonym torze)
	siła w ruchu prostoliniowym (lub w ruchu po ściśle określonym torze)
	i inne...

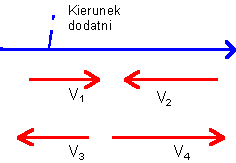
Najważniejszą różnicą między wektorem jednowymiarowym, a wartością wektora jest to, że wartość może być tylko dodatnia, a wektor jednowymiarowy może być zarówno dodatni, jak i ujemny. Mówiąc inaczej wektor wymiarowy ma swoją jedyną współrzędną równą albo plus, albo minus wartości (długości).
To jaki jest znak wektora jednowymiarowego zależy od Umowy Znaku Osi.

Umowa znaku osi

Umowa ta polega na tym, że najpierw wyróżniamy jeden zwrot (np. w prawo lub w lewo, w górę, lub w dół itp.) uznajemy jako dodatni. Jest to tzw. zwrot osi.
Od tej pory wszystkie wektory mające zwrot zgodny ze zwrotem osi będziemy traktować jako dodatnie.
Wektory przeciwne względem zwrotu osi będą miały wartości ujemne.

Przykład:
W przykładzie poniżej zwrot osi ustalamy "w prawo". Wtedy wektory narysowane na czerwono będą miały wartości jak to widać z prawej strony:

	V₁ jest dodatnie np. V₁= 4
	V₂ jest ujemne V₂= -7
	V₃ jest ujemne V₃= - 4
	V₄ jest dodatnie V₄= 8

Wektory jednowymiarowe można traktować jak zwykłe liczby - można je mnożyć jak liczby, dzielić; a nawet dzielić przez taki "wektor" (napisałem go w cudzysłowie, bo jeszcze komuś przyjdzie do głowy dzielić przez inne "prawdziwe" wektory, a to jest karalne! art. 123 par. 456, coś tam 789). Jednym słowem z tym tworem matematycznym można robić z nim wszystko co ze zwykłymi liczbami - nawet potęgować, pierwiastkować, znajdować sinusy itp.
Dzięki takiemu przedstawieniu wielkości wszystkie wzory opisujące np. ruch przyspieszony i opóźniony mają jedną wygodną postać (a nie kilka różnych z plusami i minusami do ustalenia), podobnie jednolicie można opisywać siły elektrostatyczne i wiele innych.

Wartość wektora jednowymiarowego otrzymujemy biorąc po prostu wartość bezwzględną z liczby opisującej ten wektor.

Podsumujmy zalety wektorów jednowymiarowych:

dodawanie i odejmowanie odbywa się jak zwykłe dodawanie liczb.

mnożenie skalarne to zwykłe mnożenie liczb.

wielkość ta może być umieszczana w mianowniku wzorów (można przez nią dzielić).

Większość problemów fizycznych o charakterze rachunkowym (zadań) rozwiązuje się poprzez sprowadzenie wektorów do przypadków jednowymiarowych i tam wykonywanie już rachunków w prostszej postaci - tylko na jednej współrzędnej na raz.

Dodawanie graficzne | Odejmowanie graficzne < Wektory jednowymiarowe i umowa znaku osi > Tensory - wzmianka