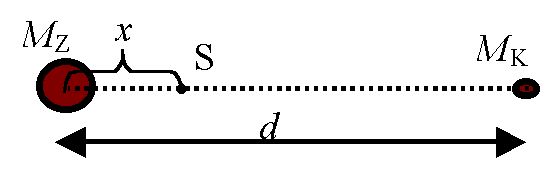Ciężar

Wzór na ciężar ciała

Ciężar właściwy

Uwagi na temat ciężaru i masy ciała

Dodatek

Uwzględnienie wpływu ruchu wirowego Ziemi

Działy i tematy powiązane

Grawitacja

Masa - podstawowe informacje

Masa, a ciężar ciała

Ciężar, a masa ciała

Duża część osób myli pojęcie masy z pojęciem ciężaru. Wynika to po części ze sposobu w jaki używamy języka potocznego, a częściowo wiąże się z metodami dokonywania pomiarów masy.

Potocznie mówimy: "Hubert waży 69 kilo”. A skoro "waży”, to by oznaczało, że ciężar wyraża się w kilogramach. Ale tak nie jest! 
Prawidłowo ciężar fizyczny powinien być wyrażany nie w kilogramach lecz niutonach!

Z określaniem ciężaru w kilogramach wiąże się stara jednostka siły – tzw. "kilogram siła” – tak określana była wartość siły, którą Ziemia przyciąga ciało o masie 1 kg. Jednak dziś nie używa się tej jednostki, bo jest ona myląca. Dlatego powinniśmy pamiętać o tej różnicy między językiem potocznym, a językiem nauki.

Podsumujmy:

	siłę ciężkości (ciężar) wyrażamy w niutonach N
	masę wyrażamy w kilogramach kg.
	dla ciał umieszczonych w pobliżu powierzchni Ziemi ciężar (liczbowo) jest ok. 10 razy większy od ich mas.

Dlaczego jeszcze nie należy utożsamiać ciężaru z masą?

Ta sama masa w różnych miejscach globu ziemskiego może mieć różny ciężar. Co prawda różnice te są niewielkie, tzn. odważnik 1 kilogramowy będzie przyciągany siłą około 10 N wszędzie przy powierzchni Ziemi. 

Jednak już nieco bardziej dokładne pomiary wykażą, że na równiku ciała są o ok. 0,3% lżejsze. 

Już znacznie mniej waży 1 kg na Księżycu – tam z racji znacznie mniejszego przyciągania grawitacyjnego srebrnego globu będzie on ok. 6 razy lżejszy niż na Ziemi, co odpowiadałoby ziemskiemu ciężarowi odważnika mającego poniżej 200 g. Gdyby jednak ten sam kilogram zważyć wagą sprężynową na Jowiszu, to okazałoby się, że jest on ponad 13 razy cięższy niż na naszej rodzimej planecie. 
Jednak we wszystkich tych miejscach masa ciężarka jest taka sama i wynosi cały czas 1 kg.

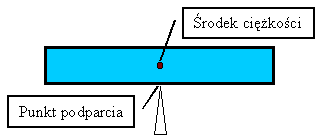
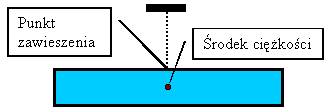
Wnioski

Punkt stabilnego podparcia

Punkt stabilnego podparcia (także zawieszenia) ciała, to taki punkt w którym ciało nie ma tendencji do przekręcania się pod wpływem sił ciężkości. Taki punkt nie jest łatwo znaleźć. Dla ciał symetrycznych znajduje się on w środku geometrycznym. 

Punkt stabilnego podarcia, a środek ciężkości

Punkt stabilnego podparcia jest ściśle związany ze środkiem ciężkości ciała. Konkretnie - punkt podparcia (lub zawieszenia) spełniający warunek stabilności (nie przewracania się, nie przekręcania pod wpływem działającej siły ciężkości) utrzymywanego przedmiotu musi znajdować się dokładnie nad, lub pod środkiem ciężkości.

Środek ciężkości

Środek ciężkości ciała, to taki szczególny punkt (czasami może on nawet nie zawierać się w obrębie ciała), że po podparciu w tym punkcie za pomocą siły przeciwnej do siły grawitacji (równoważącej tę grawitację), grawitacja nie spowoduje obrotu tego ciała. I to bez względu na początkowe ustawienie - nachylenie.

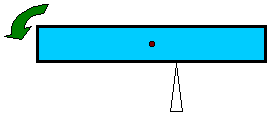
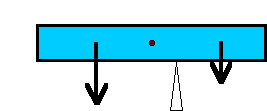
A jeśli podeprzemy ciało obok środka ciężkości?

Jeśli ciało podeprzemy obok środka ciężkości, to w większości położeń będzie się ono przekręcało albo przewracało (lub miało skłonność do przekręcania). Wynika to z faktu, żę siła ciężkości działająca z jednej strony tego ciała będzie większa, niż z drugiej i ciężar owej masy przeważy. 
Efekt ten może być osiągnięty zarówno poprzez większą ilość masy, lub tym, że masa ta jest położona dalej od punktu podparcia.

Łatwo daje się zauważyć, że środek ciężkości przedmiotów symetrycznych znajduje się w ich środku geometrycznym.

Ciekawy przykład panowania nad środkiem ciężkości można zobaczyć pod tym linkiem:

http://youtu.be/dnDeo0yhIws

Środek ciężkości, a środek masy

A środek masy?
Niemal zawsze środek ciężkości pokrywa się ze środkiem masy (wyjątek zdarzyłby się dopiero w niejednorodnym - czyli prawie niemożliwym do zaobserwowania "normalnie" - polu grawitacyjnym). 

Pojęcie środka masy jest nieco ogólniejsze od pojęcia środka ciężkości, bo ciało ma środek masy zawsze - bez względu na to, czy działa na nie siła grawitacji. Np. w stanie nieważkości trudno jest mówić o środku ciężkości, bo ciężkości ciała nie mają, natomiast środek masy jest niezmieniony. 

Dalsza interpretacja pojęcia środka masy

Środek masy możemy jeszcze wyobrażać sobie tak, że gdybyśmy w stanie nieważkości zaczęli ciągnąć ruchem przyspieszonym daną bryłę, to w wyniku takiego pociągnięcia nie nastąpi nawet chwilowe przekręcenie się ciała. 

Dzięki tym właściwościom środka masy fizykom udaje się odseparować od siebie dwie składowe ruchu bryły sztywnej:

	ruch postępowy (powiązany z ruchem środka masy)
	ruch obrotowy (dokonujący wokół środka masy).

Więcej informacji na ten temat można uzyskać wertując rozdziały poświęcone ruchowi bryły sztywnej.

Wyznaczanie środka masy (ciężkości) dla dwóch punktów materialnych

Środek masy brył jednorodnych 

W przypadku ciał symetrycznych - np. prostego, jednorodnego pręta, koła, kuli, walca, sześcianu itp., środek masy znajduje się w środku geometrycznym ciała. 

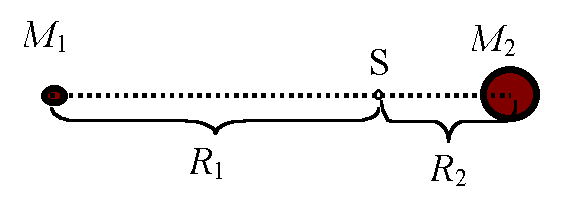
Masa rozmieszczona niesymetrycznie

Trudniej jest wyznaczyć środek masy, jeśli masa jest rozłożona nierównomiernie - czy to z powodu bardziej skomplikowanych rozmiarów, czy też z powodu niejednorodności materiału. 

Środek masy układu dwóch punktów

Jeszcze stosunkowo łatwo wyznacza się środek masy dla układu dwóch punktów materialnych.

Jest on przesunięty w stronę punktu o większej masie (idealna kula zachowuje się pod tym względem jak punkt). Dokładniej powiedzieć można, że odległości środka masy do punktów są odwrotnie proporcjonalne do mas tych punktów.

Można to zapisać wzorem:

M₁R₁ = M₂R₂

Lub, po przeniesieniu na jedną stronę wyrażenia po prawej stronie równania

M₁R₁ - M₂R₂ = 0

W przypadku bardziej skomplikowanych układów punktów materialnych zawsze musi zachodzić:

Suma iloczynów M_iR_i po lewej stronie środka masy
=
Suma iloczynów M_jR_j po prawej stronie środka masy

Lub (w bardziej "naukowym zapisie) jeśli iloczyny z lewej strony liczymy z plusem, a z prawej z minusem (albo na odwrót, bo to tylko kwestia umowy):

Σ M_i R_i = 0

Przykład – obliczanie położenia środka masy dwóch punktów

Mamy taki oto problem:
W jakiej odległości od środka Ziemi znajduje się środek masy układu Ziemi – Księżyc? Czy jest on jeszcze w środku Ziemi, czy na zewnątrz naszej planety?

Dane:

Masa Ziemi: M_z ≈ 6 ∙ 10²⁴ kg
Masa Księżyca: M_k ≈ 7.3 ∙ 10²² kg
Średnia odległość od Księżyca do Ziemi: d ≈ 3.84∙ 10⁸ m
Średni promień Ziemi: R_{Kuli_ziemskiej} ≈ 6.37∙ 10⁶ m                                                     

Szukamy:

x – odległości środka masy układu od środka Ziemi

Rozwiązanie

Z rysunku widać, że odległość Księżyca od środka masy układu wynosi

x_k = d – x

Wielkości te będziemy podstawiali do wzoru:

M_KR_K = M_ZR_Z

Przy czym:

R_z = x

R_k = x_k = d – x

Dlatego:

M_K ∙ (d - x) = M_Z ∙ x

Wymnażamy nawias:

M_K ∙ d - M_K ∙  x = M_Z ∙ x

Przenosimy M_K ∙  x na lewą stroną (z przeciwnym znakiem)

M_K ∙ d = M_Z ∙ x + M_K ∙  x

Wyciągamy x przed nawias

M_K ∙ d = (M_Z  + M_K) ∙  x

I ostatecznie dzielimy obie strony równania przez cały nawias zamieniając przy tym strony równania, aby z lewej strony mieć wielkość niewiadomą x:

Podstawiamy wielkości liczbowe:

Stąd:

x ≈ 4,6 ∙ 10⁶ m

Ponieważ średni promień Ziemi: R_{Kuli_ziemskiej} ≈ 6,37∙ 10⁶ m, więc widać, że środek masy układu Ziemia – Księżyc znajduje się we wnętrzu Ziemi (bo x < R_{Kuli_ziemskiej}).

 Jaki stąd wniosek praktyczny?
Prawie żaden. Może tylko tyle, że Ziemia wykonuje dwa ruchy obrotowe - jeden zwykły wokół swojego środka geometrycznego (też środka masy, ale samej kuli ziemskiej), a drugi ruch obrotowy, nakładający się na pierwszy, to wirowanie wokół środka masy wokół układu Ziemia - Księżyc. Może to mieć pewien wpływ na siły odśrodkowe działające na ciała na powierzchni naszej planety.