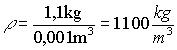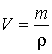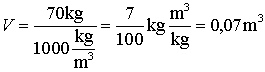: podstawy | maszyny proste | kinematyka | dynamika | termodynamika | elektryczność | fale, akustyka |

optyka | magnetyzm |  fiz. współczesna | grawitacja  | tablice | o nauce fizyki i inne | zadania  | wyszukiwanie i indeks pojęć  

aktualności ze świata  | artykuły o szkole i edukacji | nowości | O fizykonie           


Portal Fizykon.org szuka inwestorów - partnerów do współpracy                           Dane osobowe w serwisie Fizykon - informacja..

 

  

Gęstość, masa

Masa

Objętość

Gęstość

  Jednostka gęstości

  Wzór na gęstość

Przykłady

Przykłady rachunkowe

 

Czytanki - gęstość

Gęstość - przykłady rachunkowe

Przyjrzyjmy się jeszcze trochę pojęciu gęstości. Jeśli je już rozumiemy, to z łatwością odpowiemy na pytania:

Problem 1.
Który materiał z rysunku poniżej (żółty, czy czerwony) ma większą gęstość? Ile razy?

Odpowiedź:

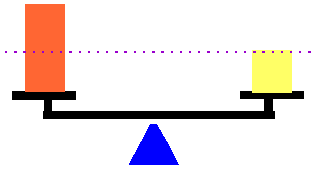Czerwony klocek ma dwa razy mniejszą gęstość niż żółty, ponieważ przy tej samej masie ma on dwa razy większą objętość.

mżółte = mczerwone
Vżółte < Vczerwone
ρżółte > ρ czerwone

 

 

 

 

Problem 2
Litr pewnego płynu ma masę 1,1 kg. Jaka jest gęstość tego płynu?

Dane jest:
masa m = 1,1 kg,
objętość V = 1l = 0,001m3.

Rozwiązanie:

Skorzystamy z definicji gęstości: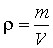

Podstawiamy dane: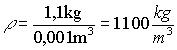

Problem 3

Gęstość aluminium wynosi około 2600 kg/m3. Jaką masę ma kostka aluminiowa o krawędzi 2 cm?

Rozwiązanie:

Ze wzoru na gęstość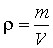

wyliczamy masę m,

Aby to zrobić, musimy pomnożyć obie strony równania przez V i podzielić przez ρ "ro". Otrzymujemy wzór w postaci:

m = ρ ∙ V

Aby otrzymać prawidłowy wynik trzeba jeszcze znaleźć objętość naszej kostki. Oczywiście skorzystamy ze wzoru na objętość sześcianu:

V = a3

Po podstawieniu do wzoru na gęstość będziemy mieli:

m = ρ ∙ a3
To jest wzór wynikowy!

Dane liczbowe muszą być wyrażone w takich jednostkach, aby metry sześcienne w definicji gęstości skróciły się z metrami sześciennymi objętości. Dlatego krawędź sześcianu wyrazimy w metrach:

a = 2 cm = 0,02 m

Podstawiamy dane liczbowe

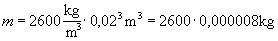
trochę przekształcimy..
to są ostatnie przekształcenia...

m = 26 ∙0,0008kg=0,0208kg

I wreszcie...
Przybliżony wynik liczbowy:

m = 21 g  

i na koniec odpowiedź słowna:
Nasza kostka aluminiowa waży około 21 gramów (tyle co jedna piąta zwykłej tabliczki czekolady).

Problem 4

Jaka jest objętość człowieka o masie 70 kg? (Wskazówka: załóż, że średnia gęstość ciała ludzkiego jest równa gęstości wody, czyli 1000 kg/m3)

Rozwiązanie:

Wykorzystamy wzór na gęstość:
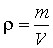trzeba go przekształcić tak, aby otrzymać z niego objętość. Zrobimy to dzieląc obie strony równania przez  ρ i mnożąc przez V. Stąd:
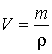Po podstawieniu danych liczbowych otrzymamy:

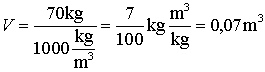Inne obliczenia z użyciem gęstości
Wiedząc jaka jest masa 1 m3 materiału można łatwo obliczyć jaką masę ma inna objętość tego materiału.
Wystarczy ze wzoru na gęstość obliczyć masę

m = ρ ∙ V

Przykłady:

a) Jaką masę ma 1 litr wody (gęstość wody to 1000 kg/m3)?

Rozwiązanie:

Ponieważ 1 litr to 0,001 m3,

więc masa tej wody to: m = 1000∙ 0,001 = 1 kg.

b) Jaką masę miałby kieliszek 50ml wypełniony złotem?
Dane: Szukamy:

V  = 50 ml = 0,05 l = 0,00 005 m3 = 5∙ 10-5 m3.

 ρ złota = 19300 kg/m3

 masa m
Rozwiązanie:

m = ρ ∙ V = 19300 ∙ 0,00005 = 0,965 kg 

Ciekawe...

 Mały kieliszek złota waży prawie kilogram.