| Wielkość wyznaczana / nazwa wzoru |
wzór |
co we wzorze |
| I zasada termodynamiki |
∆U = Q + W
|
∆U - przyrost energii wewnętrznej układu
Q - ciepło dostarczone do układu
W - praca wykonana nad układem |
Energia wewnętrzna gazu doskonałego
Energia nie oddziałujących ze sobą cząsteczek gazu |
U = cv n T
|
U - energia wewnętrzna
R - stała gazowa
n – liczba moli gazu
T – temperatura bezwzględna (w kelwinach)
|
| Energia ogrzewania (ochładzania) ciała - bez przemian
fazowych (czyli bez topnienia, krzepnięcia, parowania, krystalizacji
itp.) |
Q = m cwł ∆t
Q = m cwł ∆T
Q = n c ∆t
Q = n c ∆T
|
Q – wymieniane ciepło
m – masa
t – temperatura w °C
T – temperatura bezwzględna (w kelwinach)
c - ciepło molowe w układzie SI w J/molK |
| Energia potrzebna do zajścia przemian fazowych |
Q = m·cprzemiany
Przykładowo:
Q = m·Rp
Q = m·L
|
cprzemiany– ciepło danej
przemiany fazowej np.
L - ciepło topnienia
Rp - ciepło parowania |
Stała gazowa R
R = 8,31 J/mol·K |
R = k·NA
|
k = 1,38054·10-23 J/K
NA= 6,02·1023 1/mol |
| Praca w przemianie izobarycznej |
W = – p ∆V
|
V - objętość
p – ciśnienie
minus wynika z faktu, że wzrost objętości oznacza oddawanie energii
przez układ (gaz) |
| Równanie Clapeyrona (stanu gazu doskonałego) |
p V = n R T
|
symbole - j.w. |
| Związek między Cp i CV |
Cp = CV
+ R
|
Cp ciepło molowe przy stałym ciśnieniu
CV - ciepło molowe przy stałej objętości |
Równanie przemiany izotermicznej gazu doskonałego
(T = const)
Prawo Boyle'a i Mariotte'a |
p ∙ V = const
p1∙V1 = p2∙V 2
|
p1, V1 - ciśnienie i
objętość w momencie 1
p2, V2 - ciśnienie i objętość
w momencie 2
|
Równanie przemiany izobarycznej gazu doskonałego
(p = const)
prawo Gay Lussaca
|
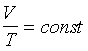
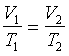 |
V1, T1 - objętość i
temperatura (w Kelwinach) w momencie 1
V2, T2 - objętość i
temperatura (w Kelwinach) w momencie 2
|
|
Równanie przemiany izochorycznej gazu doskonałego
(V = const)
Prawo Charlesa
|
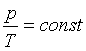
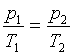 |
p1, T1 - ciśnienie i
temperatura (w Kelwinach) w momencie 1
p2, T2 - ciśnienie i temperatura
(w Kelwinach) w momencie 2
|
Równanie przemiany adiabatycznej gazu doskonałego
(brak wymiany ciepła z otoczeniem Q = 0) |
p ∙ Vχ
= const
p1∙ V1χ
= p2
∙V2χ
|
χ - stosunek Cp/CV – współczynnik
adiabaty zależny od ilości stopni swobody cząsteczek gazu. |
|
Stosunek ciepła właściwego przy stałym ciśnieniu,
do ciepła właściwego przy stałej objętności (wykładnik adiabaty)
|
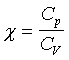 |
Dla gazów doskonałych o cząsteczkach :
jednoatomowych: χ = R∙3/5
dwuatomowych: χ = R∙5/7
trzyatomowych: χ = R∙3/4
|
| Zależność między energią kinetyczną cząsteczek gazu
doskonałego a temperaturą dla gazu jednoatomowego. |
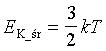 |
k - stała Boltzmanna
k = 1,38054*10-23
T - temperatura w Kelwinach |