|
|
Układ biegunowy (walcowy)Układ biegunowy (w odniesieniu do rozważań przestrzennych nazywany "walcowym") jest wygodny do stosowania wtedy, gdy analizujemy obroty ciał. W układzie tym zamiast posługiwać się współrzędnymi X i Y (i w przestrzeni Z), wprowadza się dwie współrzędne innego rodzaju:
Układ biegunowy jest wygodny, gdy trzeba opisywać ruchy obrotowe. Po umieszczeniu środka układu współrzędnych dokładnie w osi obrotu (prostopadłej do płaszczyzny obrotu) promień wodzący dla danego punktu jest stały. Wtedy dość często ruch może być opisywany tylko za pomocą zmian tylko jednej współrzędnej – kąta φ.
Przekształcenie odwrotne wygląda następująco:
Patrz także: Układ odniesienia, Układ kartezjański, Rozważania o pojęciu układu odniesienia
|
||||||
|
|
|||||||
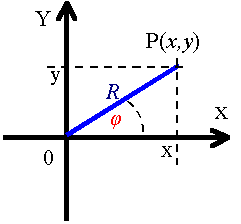 Pomiędzy
współrzędnymi w układzie biegunowym i kartezjańskim zachodzą proste
związki:
Pomiędzy
współrzędnymi w układzie biegunowym i kartezjańskim zachodzą proste
związki: