|
|
Oczko prądu, czyli drugie sformułowanie II prawa KirchhoffaII prawo Kirchhoffa można sformułować także nieco inaczej – nieco bardziej „matematycznie” i ogólnie. Oczko prąduWyobraźmy sobie, że mamy jakiś fragment obwodu, który zawiera źródła prądu oraz odbiorniki (oporniki). Jeśli taki fragment stanowi obwód zamknięty, to będziemy go nazywać „oczkiem” prądu. W naszym przypadku w oczkach wystąpią ogniwa charakteryzowane przez siłę elektromotoryczną i opór wewnętrzny, a jako odbiorniki prądu będziemy mieli oporniki o znanym oporze.
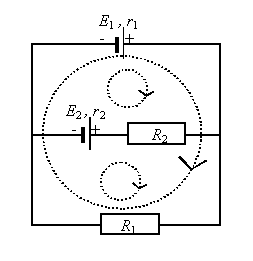
Na powyższym rysunku można zauważyć trzy oczka (symbolizowane przez kółka rysowane linią przerywaną) – dwa mniejsze i jedno większe, obejmujące poprzednie oczka.
Dla oczek został zaznaczony kierunek ich obiegu – w tym wypadku wszystkie oczka mają kierunek obiegu zgodny z kierunkiem obiegu zegara. Jednak można ustalić sobie przeciwny kierunek obiegu. Zliczanie napięć w oczku prąduZastosowanie prawa Kirchhoffa w ujęciu oczkowym będzie polegało na
zliczaniu napięć podczas poruszania się zgodnie z ustalonym kierunkiem
obiegu oczka.
W „oczkowym” sformułowaniu II prawo Kirchhoffa będzie miało postać: W oczku prąd suma spadków napięć na wszystkich odbiornikach prądu musi być równa zeru. Można to zapisać wzorem:
Przykład
Po uwzględnieniu tych oznaczeń, II prawo Kirchhoffa przybierze postać równań. Dla pierwszego małego (górnego) oczka: E1 – I1 ∙ r1 + I2 ∙ R2 – E2 + I2 ∙ r2 = 0 Dla drugiego małego (dolnego) oczka: E2 – I2 ∙ r2 – I2 ∙ R2 – I3 ∙ R1 = 0 Dla dużego oczka (przy rozwiązywaniu obwodów, trzecie równanie jest już nadmiarowe i nie należy go dołączać do zestawu, jeśli poprzednie wszystkie zostały wykorzystane): E1 – I1 ∙ r1 – I3 ∙ R1 = 0
|
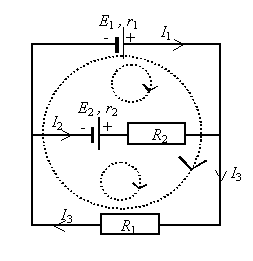 Dla obwodu przedstawionego
wcześniej, aby poprawnie
zastosować II prawo Kirchhoffa, należy oznaczyć kierunki (niekoniecznie
muszą one ostatecznie okazać się zgodne z rzeczywistością) prądów.
Zostało to zrobione na rysunku obok.
Dla obwodu przedstawionego
wcześniej, aby poprawnie
zastosować II prawo Kirchhoffa, należy oznaczyć kierunki (niekoniecznie
muszą one ostatecznie okazać się zgodne z rzeczywistością) prądów.
Zostało to zrobione na rysunku obok.