Nacisk - przykłady 2

Najpierw weźmiemy się za górny klocek – tutaj sytuacja jest identyczna jak w problemie rozważanym poprzednio. Dlatego już bez zbytnich dywagacji napiszemy:

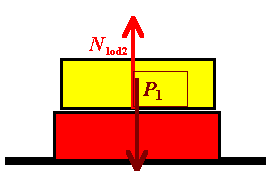
Na klocek 1 działają dwie siły:

	Siła ciężkości o wartości P₁ = m₁·g skierowana w dół
	Siła nacisku od klocka dolnego. Siła ta jest skierowana do góry i musi zrównoważyć ciężar 1. Jej wartość: N_1od2 = m₁·g

Powyższe siły się równoważą (wartości obu sił są równe), więc klocek nie porusza się.

Klocek 2

Teraz rozważymy siły działające na klocek 2 (czerwony). Działają tu trzy siły:

Siła ciężkości P₂ tego klocka (skierowana w dół)

Siła nacisku pochodząca od klocka 1, czyli N_2od1 (skierowana w dół)

Siła nacisku pochodząca od dolnej powierzchni, czyli N_{2od_Pow} (skierowana w górę)

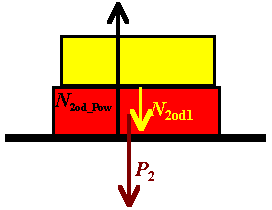Wartości tych sił są następujące:

Siła ciężkości P₂ = m₂· g
Siła nacisku od klocka 1 (górnego) jest równa co do wartości sile, jaką klocek 2 działa na klocek 1 – wynika to z III zasady dynamiki Newtona. Można więc napisać:
N_2od1 = N_1od2 = m₁·g
Siła nacisku powierzchni na klocek 2 musi zrównoważyć ciężar obu znajdujących się nad nią ciał, czyli jest sumą obu tych sił ciężkości:

N_{2od_Pow} = P₁ + P₂ = m₁·g + m₂·g=( m₁ + m₂)·g.

Oczywiście siła nacisku od powierzchni (skierowana do góry) równoważy obie siły działające w dół. Dzięki temu powyższy klocek też pozostaje w równowadze.

N_{2od_Pow} = N_2od1 + P₂

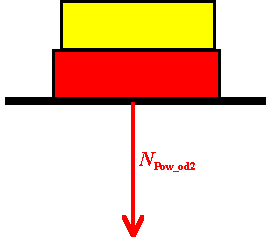
Siły działające na powierzchnię

Na powierzchnię działa od góry nacisk pochodzący od klocka 2. Jego wartość jest równa ciężarowi obu klocków: 1 i 2

N_{Pow_od2} = P₁ + P₂ = m₁·g + m₂·g

Wyciągamy g przed nawias:

N_{Pow_od2}=( m₁ + m₂)·g

Wnikliwy czytelnik zapewne zauważy:

to jak to... działa tylko jedna siła? – przecież pod jej wpływem powierzchnia powinna przyspieszać w dół?...

- no cóż, słuszna uwaga. Musi więc istnieć jakaś dodatkowa, nieznana siła, która z kolei tę powierzchnię utrzymuje w równowadze. Ta ukryta siła równoważy zarówno siłę nacisku od klocka 2, jak też ciężar materiału, z którego wykonano powierzchnię. Ale tą ostatnią siłą nie będziemy już się zajmować.