Kąt w radianach

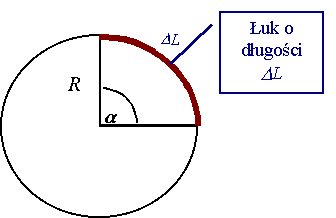
Ponieważ tor poruszającego się punktu jest całkowicie wyznaczony kształtem okręgu, można tak zmienić sposób opisu, że będzie on prostszy. Dodatkową zaletą opisu w układzie biegunowym, jest fakt, że dla całkowitego przekazania informacji o położeniu wystarczy podanie tylko jednej zmiennej (plus najczęściej stały promień okręgu R).

Tą dobrą zmienną może być np. długość drogi przebytej wzdłuż okręgu ∆L, lub (co się częściej stosuje) - kąt obrotu α (ew. ∆α).

Znaczenie symboli:
∆α, α – kąt (w układzie SI w radianach, co jest równoważne wielkości niemianowanej)
∆L – długość drogi przebytej wzdłuż łuku okręgu (w układzie SI w metrach m)
R – promień okręgu którego fragmentem jest zakreślany łuk (w układzie SI w metrach m).

Powyższy wzór może być uznany za definicję kąta wyrażonego w radianach. Dlatego warto go zapamiętać.

Dlaczego używa się jednostki radian?

Mamy przecież inną jednostkę - stopień °...
Odpowiedź wynika z dalszych zastosowań. "Siła" radianów objawia się przy zastosowaniu używanych funkcji trygonometrycznych - sinus, kosinus, tangens.
Radiany mają jedną wielką zaletę w porównaniu z miarą w stopniach. Otóż dla małych kątów sinus kąta w radianach i tangens kąta, są w przybliżeniu równe samemu kątowi.

Inaczej mówiąc dla małych kątów obowiązuje zależność:

sin x ≈ tg x ≈ x

Obowiązuje to z różnym przybliżeniem w zależności od wartości kąta x. Im mniejszy kąt, tym lepsze przybliżenie. Poniższa tabelka pokazuje opisany związek na przykładach (więcej informacji o przeliczaniu stopni na radiany znajduje się w rozdziale przeliczenia stopni na radiany i radianów na stopnie):

x w °

x w rad

sin x

tg x

dokładność przybliżenia

0

0

0

0

dokładność 100% - owa

1

0,017453293

0,017452406

0,017455065

błąd rzędu 0,01 %

3

0,052359878

0,052335956

0,052407779

błąd rzędu 0,1 %

5

0,087266463

0,087155743

0,087488664

błąd rzędu 0,3 %

8

0,13962634

0,139173101

0,140540835

błąd rzędu 1%

10

0,174532925

0,173648178

0,176326981

błąd rzędu 1,5%

15

0,261799388

0,258819045

0,267949192

błąd rzędu 3,5%

30

0,523598776

0,5

0,577350269

błąd rzędu 15 %

45

0,785398163

0,707106781

1

błąd rzędu 37%

60

1,047197551

0,866025404

1,732050808

błąd rzędu 82%

75

1,308996939

0,965925826

3,732050808

błąd rzędu 211%

Jak widać z powyższej tabelki dokładność przyjęcia kąta w radianach równego sinusowi i tangensowi sprawdza się bardzo dobrze do ok. 3° - 5°, dobrze do 8° (1% błędu). "Z grubsza" można tę przybliżoną równość uznawać dla kątów rzędu kilkunastu stopni.
Dla kątów na poziomie kilkudziesięciu stopni przybliżenie zupełnie zawodzi.

Można więc powiedzieć, że określenie dla małych kątów oznacza:

	kąt do 5° jeśli chcemy mieć bardzo dobrą dokładność,
	kąt do 8° jeśli zupełnie niezłą dokładność,
	do 15° dla już dość wyraźnego przybliżenia,
	do 30° - jeśli chcemy mieć tylko zgrubną orientację.

Uwaga:
W poniższej tabelce dokładność przybliżenia związana jest z najbardziej "niekorzystnym przypadkiem", czyli gdy próbujemy sinusa kąt uznać za równego tangensowi. Dlatego błąd tu jest duży.

W przypadku gdy stosujemy przybliżenie tylko dla sinusa: sin x ≈ x
wtedy błędy dla małych kątów są mniejsze, a dla kątów do 14° nie przekraczają 1%.

Wstęp < Kat w radianach > Prędkość kątowa