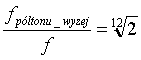Muzyka - interwały

Tabela częstotliwości tonów

Rytm w muzyce

Strojenie instrumentów

Muzyka - uzupełnienia

Interwały, częstotliwości dźwięków muzycznych

Osoby znające się na muzyce zadają sobie nieraz pytanie:
Jak przekłada się częstotliwość tonu na standardową notację muzyczną. Inaczej mówiąc jaką częstotliwość ma np. dźwięk c'?

Obliczenie częstotliwości tonu podstawowego dowolnej nuty nie jest wcale trudne. Wystarczy tylko wiedzieć, że:

	podstawową częstotliwością do której stroi się wszystkie instrumenty jest częstotliwość dźwięku a' (a razkreślne) - wynosi ona 440 Hz.
	zmiana o jedną oktawę odpowiada przyrostowi (lub zmaleniu) częstotliwości o czynnik 2 - czyli skoro a' ma 440 Hz, to a2 ma 880 Hz, a3 - 1760 Hz itd.
	interwały mniejsze niż oktawa da się wyliczyć znajdując iloraz częstotliwości dla pojedynczego półtonu. Ponieważ półtonów w oktawie jest 12, to 12 krotne pomnożenie przez ów iloraz musi dać 2 (tak jak dla oktawy). Stąd w sposób oczywisty wynika, że półtonowy interwał odpowiada ilorazowi częstotliwości równemu pierwiastkowi 12-ego stopnia z 2.

Wartość ta wynosi ok. 1,059463 (Oczywiście: 1,059463¹² = 2).

Jak teraz, dzięki tym informacjom, obliczyć np. częstotliwość dźwięku c² – czyli dźwięku c (Do) następującego najbliżej po kamertonowym a’?

Ustalmy:
- a¹ od c² dzielą 3 półtony (a-b, b-h, h-c).

Dlatego:

Zatem częstotliwość tonu podstawowego dźwięku c² wynosi 523,25 Hz.
Częstotliwość tonu c¹ będzie oczywiście o połowę mniejsza, czyli będzie wynosiła ok.:  262 Hz.

Muzyka - interwały << Tabela częstotliwości tonów

Rozdziały powiązane: dźwięk - co to jest