Wyrażanie wartości sił składowych przez funkcje trygonometryczne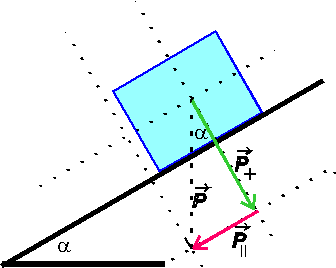

Przypatrzmy się jeszcze raz rozkładowi siły ciężkości na składowe. Rysunek obok jest podobny do zrobionego w rozdziale poprzednim z wyjątkiem umiejscowienia siły ściągającej P_||. Została ona przeniesiona do końca siły ciężkości, tak aby wraz ze składową prostopadłą utworzyć trójkąt prostokątny.

Kąt ostry tego trójkąta jest równy kątowi nachylenia równi (kąty o ramionach prostopadłych są równe)

Teraz będziemy mogli siły P₊ i P_|| wyrazić przez daną wartość ogólną siły ciężkości P.

Korzystając z definicji funkcji trygonometrycznych sinus i kosinus można napisać związek pomiędzy siłą ciężkości i jej składową równoległą do równi:

stąd:

P_|| =P ∙ sin α

Teraz powiążemy wartość składowej prostopadłej z siłą ciężkości P.

stąd:

P₊ =P ∙ cos α

Wartości na P_|| i P₊ przydadzą nam się następnie do ostatecznych obliczeń na siłę wypadkową.