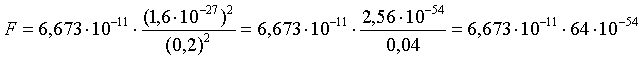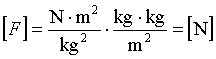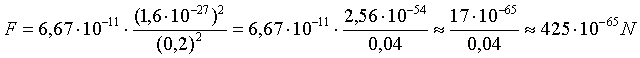O zaokrąglaniu liczb we wzorach(aktualnie rozpatrywany jest przypadek gdy wzory zawierają tylko mnożenie i
dzielenie) Powiązane rozdziały:Odczytywanie i interpretowanie
wzorów fizycznych
| |
|
„...na kartkówce z oddziaływań dostałem następujące zadanie: Oblicz siłę grawitacji działającą między dwoma protonami znajdującymi się w odległości 20 cm od siebie. Wziąłem się więc do pracy. |
|||||||||||||||||
|
Uwagi od autora artykułu: |
|||||||||||||||||
|
Najpierw wypisałem dane: G = 6,673 ·10-11 |
Paweł źle zaokrąglił masę protonu, bo wynosi ona 1.67239·10-27 kg, czyli powinna być zaokrąglona w górę – do 1,7·10-27 |
||||||||||||||||
|
Wzór: |
Paweł zastosował skrót myślowy, ponieważ m1 = m2 = Mp. |
||||||||||||||||
|
Zacząłem podstawiać do wzoru:
F = 6,673·10-11·64·10-54 F = 427,072·10-65 N
bo (ze
wzoru jednostkowego): Natomiast druga wersja różni się tylko dokładnością podstawienia G:
Koniec tekstu Pawła. |
|||||||||||||||||
|
Teraz będzie dłuuuugi komentarz.W tym co Paweł napisał widać kilka rzeczy
– po pierwsze: na pewno rozumie, jakie liczby podstawić i do
jakiego wzoru. Prawidłowo podstawił do wzoru za m1 i
m2 masę protonu. Paweł umie też przekształcać potęgi
(w oryginalnym mailu był błąd w zapisie obliczeń, ale wyglądający
ewidentnie na pomyłkę „w druku”). Dlatego najpierw postawmy sobie pierwsze bardzo istotne pytanie: Jaką dokładność mają dane w tym zadaniu?Zacznijmy od podanego promienia: r = 20 cm.Pozornie nie posiadamy żadnych danych, które umożliwiłyby nam określenie
dokładności
tej liczby. Czyżby więc odległość wynosiła dokładnie
20 cm i ani mikrona więcej?
- Ja wyciągam z powyższego zapisu wniosek, że rozpiętość wartości
tej
danej wynosi w rzeczywistości 1 cm. Dlaczego?
A ile było przed zaokrągleniem? Ktoś mógłby powiedzieć – ale może w istocie ta dana jest
dokładniejsza? Popatrzmy na kolejne dane:
Tutaj Paweł wypisał aż 4 cyfry znaczące. Bez znajomości dokładnej wartości tablicowej możemy tylko wnioskować, że ostatnia cyfra (3) z wypisanych czterech cyfr znaczących jest „niepewna” na poziomie od 0,0025 ·10-11 do 0,00349999 ·10-11... . Dokładność procentowa podania stałej G wynosi zatem 0,0005 dzielone przez 6,67, czyli 0,00007 (czynnika 10-11 nie uwzględniamy bo i tak się skraca). Jest to błąd procentowy zdecydowanie poniżej promila, czyli znacznie mniejszy niż błąd dla odległości r. Teraz dokładność masy (poprawmy tu od razu błąd Pawła i zaokrąglijmy poprawnie): Mp = 1,67239·10-27 kg ≈ 1,7·10-27 kg Tutaj możemy wręcz obliczyć dokładność zaokrąglenia – od 1,7 do wartości dokładnej 1,67239 jest ok. 0,028, co po podzieleniu przez 1,7 da nam 0,016 – błąd zaokrąglenia jest na poziomie 1,6% (dziesięć do potęgi -27 przy dzieleniu znowu się skraca więc ten czynnik od początku nie był uwzględniany). Ustaliliśmy jako tako dokładność danych. Jednak to nie koniec problemu. Bo pojawia się tu pytanie: Która liczba na największy wpływ na dokładność wyniku?Myślę, że chwila zastanowienia się doprowadzi nas niechybnie do wniosku, że:
Co z tego, że w pewnym wzorze dla jakiejś tam wartości biedzimy się
nad piątym miejscem po przecinku, jeśli dla innej danej w tym wzorze
niedokładna jest już pierwsza cyfra? Potem będziemy te liczby mnożyć
przez siebie (i dzielić). I jeżeli jeden ze składników iloczynu
"waha" się od 1,2 do 1,3, to oczywiście cały wynik też się
będzie "wahał" w podobny sposób w jego "takt". A
to, że inna dana się prawie nie "waha", to nie poprawia nam
niestety problemu ostatecznej dokładności wyniku. Dlatego w naszym przypadku, na pewno nie ma sensu podstawiać do wzoru tak dokładnej wartości G (dokładnej jak to zapisano wyżej) – wystarczyłaby np. dokładność 10 – krotnie mniejsza. A masa protonu Mp – jaki ma wpływ na błąd? - Błąd na poziomie 1,6% wobec 2,5% najmniej dokładnej danej to właściwie też już „coś”. Dlatego być może w bardzo dokładnych badaniach w podobnych obliczeniach należałoby zaokrąglić tę masę nieco precyzyjniej – do 1,67·10-27 kg. Ale już na pewno nie bardziej – bo i tak decyduje ta najmniej dokładna dana - czyli w tym wypadku r. Ale to niestety, jeszcze nie koniec problemów...Muszę tu wspomnieć jednak o jeszcze jednej ważnej sprawie – pewnej mojej (świadomej – bo nie o wszystkim da się powiedzieć na raz) nieścisłości. W rzeczywistości, znaczenie błędów wstawianych wartości jest dla tego wzoru jest trochę bardziej skomplikowane, niż to wyżej napisano. A wszystko za przyczyną potęg. Problem w tym, że liczb w naszym wzorze A to powoduje, że znaczenie błędu wielkości ich odpowiadających podwaja się (w przypadku wyrażenia zawierającego wyłącznie dzielenia i mnożenie znaczenie błędu mnoży się przez wykładnik potęgi). Zatem dla wyniku końcowego nasze błędy będą już inne:
Jak z tego widać, trzeba oszacować błąd wyniku jako większy niż 5%. Oznacza to, że ostatecznie nie ma sensu podawać więcej niż 2 cyfry znaczące wyniku, bo druga z nich jest już i tak w znacznym stopniu niepewna. Liczby, które są podnoszone do potęgi należy podstawiać do wzoru z większą dokładnością, aby przez podniesieniu błędu do potęgi nie spowodować wzmocnienia jego roli. Oczywiście wiele osób cały czas gnębi wątpliwość: A właśnie że zaszkodzi!!! Bo jeśli ktoś znający się na rzeczy zacznie wyciągać wnioski na temat dokładności z ilości cyfr podanej mu liczby (właśnie tak jak to opisano przy okazji omawiania dokładności promienia r), to będą one nieprawidłowe. Czyli: Poprawne jest zaokrąglenie wyniku końcowego tylko do tej cyfry, która jest już niepewna, ale jeszcze „z grubsza” określona. Podawanie większej ilości cyfr nie będzie oznaczało większej rzetelności i dokładności, lecz odwrotnie! – będzie oszukiwaniem czytającego - sugerowaniem mu, że wynik jest dokładniejszy niż to jest w istocie. I jest to jednocześnie dawanie świadectwa własnej ignorancji dotyczącej podawania danych.
|
|||||||||||||||||
Jak podawać poprawnie wyniki?Z grubsza można przyjąć regułę, że wynik podajemy z dokładnością tylu cyfr znaczących aby dojść do pierwszej która jest już niedokładna (ale jeszcze coś tam do naszej wiedzy o wyniku wnosi). W naszym wypadku najmniej dokładne było podanie odległości – dwie cyfry znaczące. I do tylu cyfr znaczących należałoby zaokrąglić wynik. Tak więc, chociaż z kalkulatora odczytałem liczbę: F = 4,665908926660825 ·10-63 to moim wynikiem jest F = 4,7 ·10-63 Wyniki podane przez Pawła:
wykazują za to wyraźnie co się dzieje, gdy źle zaokrąglamy liczby we wzorach.
Warto zaznaczyć, że w wynikach Pawła, trzecia cyfra znacząca
w tych wynikach i tak jest... Uwaga odnosząca się do samego zapisu liczb z potęgamiPodawanie liczb zawierających
mnożenie przez 10 do potęgi powinno spełniać pewien przyjęty przez
fizyków standard: Zawsze przekształcić zapis liczby w ten sposób, bo „10 do potęgi ...” może „wchłonąć” dowolne przesunięcie przecinka w liczbie poprzedzającej potęgę dziesiątki. Dzięki takiemu zapisowi liczb, łatwo jest je porównywać - nie musimy pracowicie liczyć zer przed, czy po przecinku, ale patrzymy na wykładniki - jeśli się różnią, to już wiadomo, która liczba jest większa, a jeśli są takie same, to wszystko widać po liczbie występującej przed potęgą dziesiątki.
Recepta na prawidłowe podstawianie liczb do wzorów i wykonywanie przekształceńZbierzmy wnioski, które nasunęły się przy analizie rozwiązania Pawła. Przedstawię je w postaci dość uproszczonych zasad związanych z podstawianiem liczb do wzorów, wykonywaniem przekształceń i prezentacją wyniku końcowego. Sposób postępowania w przypadku gdy we wzorze są jedynie działania mnożenia i dzielenia i gdy chcemy osiągnąć maksymalną dokładność wyniku końcowego:
W ten sposób szansa, że coś "uronimy" z dokładności danych jest minimalna, jako że wykonujemy działania i tak z nadmiarową dokładnością. Jednocześnie nie będziemy męczyć się nadmiarem cyfr do przeliczeń i nie wprowadzimy w błąd osoby odczytującej nasz wynik. Oczywiście czasami jest tak, że nasza oczekiwana od wyniku dokładność jest mniejsza niż ta, którą możemy osiągnąć. Wtedy już wcześniej można zmniejszyć dokładność przekształceń, dostosowując ją do zamierzonego celu. Przykład:Dane są trzy liczby:
Mamy je podstawić do wzoru:
Oczywiście jeżeli i tak wykonujemy obliczenia na kalkulatorze, to nie musimy za każdym razem po kolei zaokrąglać wyników cząstkowych (można wtedy zaokrąglać liczby dopiero tam, gdzie jest to wygodne). Ważne jest, aby wszędzie tam gdzie się ten wynik cząstkowy pojawia, nie zmniejszyć jego dokładności, ani też nie męczyć się z nawałem niepotrzebnych, w rzeczywistości nic nie znaczących cyfr. Na koniec zastrzeżenie!Powyższe rozważania odnosiły się wyłącznie do wzorów
zawierających tylko działania mnożenia i dzielenia (podnoszenie od
potęgi można potraktować jako wielokrotne mnożenie lub dzielenie).
Jednak jeśli wzór zawiera sumy, różnice, funkcje trygonometryczne,
logarytmy i inne matematyczne komplikacje, to opisane tu proste reguły
przestaną być słuszne. |
|||||||||||||||||
Patrz także:Odczytywanie i interpretowanie
wzorów fizycznych
|
|||||||||||||||||

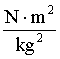
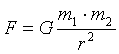
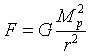 - i jest to ostateczny
wzór do którego są podstawiane dane..
- i jest to ostateczny
wzór do którego są podstawiane dane..