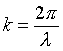Równanie harmonicznej fali płaskiej
|
|||||
Równanie fali harmonicznej płaskiej ma postać:
|
|||||
|
ω - częstość kołowa
T - okres drgań |
k - liczba falowa
Stosuje się też pojęcie "wektora falowego" - dla fali rozchodzącej się w trzech wymiarach. Wektor falowy ma kierunek zgodny z kierunkiem rozchodzenia się fali i wartość daną przez k. |
||||
Interpretacja równania faliRównanie fali łączy w jedno dwa wymiary związane z ruchem falowym
Koralik na animacji wyżej jest położony w jednym miejscu (licząc w poziomie) i może wykonywać ruchy pionowe wymuszane przez falę. Fala wymusza na koraliku drgania (fala harmoniczna, wymusza drgania harmoniczne). W podobny sposób jak koralik zachowują się wszystkie punkty ośrodka, do których dociera fala. |
|||||
|
Polaryzacja << Równanie fali płaskiej >> Prędkość fali |
|||||