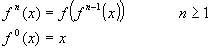Teoria chaosu

Autor tekstu: Sebastian Małyska

Wstęp

W naszym potocznym rozumieniu chaos to coś niedobrego; coś, na co raczej nie czekamy - więcej: przeraża nas myśl o społecznym chaosie, o chaotycznie pracującej elektrowni atomowej itd. Myśląc o chaosie, myślimy wręcz o katastrofie. Chcielibyśmy mieć świat i wyobrażenie o nim uporządkowane, stałe i niezmienne. Jedni z nas widzą świat mimo wszystko uporządkowany i niezmienny, możliwy do opanowania, i to bez poszukiwania nowych środków i narzędzi, drudzy - wręcz przeciwnie: jako kłębowisko sił i energii, których potęga zdaje się przerastać nasze możliwości, lecz jednocześnie stanowi wyzwanie dla umysłu człowieka.

Lecz dzisiaj tego typu "jednoznaczne" teoria, założenia i wynikające zeń "pewniki" zostają bardzo poważnie poddane w wątpliwość. Powód? Przemożny wpływ (naturalnie nie zawsze przecież uświadamiany) Teorii Chaosu. Dzisiejsza nauka, zwana też „nową nauką”, odchodzi i przekracza dotychczasową wiedzę wraz z jej tradycyjnymi aksjomatami i porusza się po obszarach, które laikowi wydawać się muszą "paranormalne". Naukowcy też mają swe przekonania, lecz trudno je nazwać wiarą - trudno w coś wierzyć, gdy się to wie... Teoria Chaosu - która opiera się na założeniu, iż możliwe jest dokonywanie pomiarów, kontrolowanie lub odtwarzanie matematycznie nieprzewidywalnego zachowania się układów lub przebiegu zjawisk (procesy chaotyczne można zaobserwować np. w przebiegu zjawisk atmosferycznych bądź w turbulencjach ruchliwych cieczy, kiedy to ledwie dostrzegalne zakłócenia warunków początkowych powodują znaczące zmiany w końcowych stadiach ruchu; istnieje poetyczna wizja motylego skrzydła, które wprawione w ruch w Afryce wpływa na przebieg globalnych zjawisk klimatycznych) - po prostu dezaktualizuje większość naszych dotychczasowych poglądów, przekonań i tradycyjnych wiar zbudowanych na starych paradygmatach, zupełnie nieprzystawalnych jako narzędzia do dzisiejszych problemów, potrzeb, pytań i odkryć.

Dlaczego tak się dzieje? Co się stało? Otóż "odpowiedzialne" są tu pospołu: fizyka kwantowa, relatywizm nauki, zasada nieokreśloności Wernera Heisenberga (teoria mówiąca, iż obserwacja danego procesu nieuchronnie oddziałuje na ten proces, a zatem wyniki takiej obserwacji są zawsze wartościami relatywnymi, nie absolutnymi), zasada antropiczna (zespół teorii fizycznych i kosmologicznych głoszących, że obecność człowieka (gr. anthropos) we wszechświecie nie jest przypadkowa, a człowiek jako obserwator kosmosu jest czynnikiem determinującym prawdopodobieństwo w fizyce, ma on też zasadniczy wpływ na powstawanie rozmaitych zjawisk we wszechświecie, przetwarza i przekazuje informacje, co byłoby potwierdzeniem Einsteinowskiej koncepcji czasoprzestrzeni), a także wynikająca z tego wszystkiego "nowa kosmologia".

Chaos na gruncie nauk ścisłych

Teoria chaosu stała się jedną z trzech (obok Teorii Względności i Mechaniki Kwantowej) największą rewolucją w nauce XX wieku, jednak w odróżnieniu od wyżej wymienionych dotyczy ona wszystkiego (tamte odpowiednio: fizyki; fizyki, chemii, biologii). Rewolucja ta polegała na odkryciu że bardzo proste formuły matematyczne prowadzą do chaosu (wcześniej uważano że układy są skomplikowane ponieważ opisują je skomplikowane formuły matematyczne.

Dokonując analizy wyłącznie na bazie fizyki (szczególnie dynamiki) rozróżniamy trzy możliwe typy zachowań układów dynamicznych: periodyczne (włączając tu niezależne od czasu), quasiperiodyczne i chaotyczne. Zachowanie quasiperiodyczne jest złożeniem przebiegów periodycznych o niewspółmiernych częstościach.

Zachowanie chaotyczne charakteryzuje się niestabilnością (brakiem stanu równowagi, nie trwałością) rozwiązań równania ruchu ze względu na warunki początkowe. Oznacza to, że dowolnie mała zmiana stanu początkowego prowadzi po jakimś czasie do jakościowych zmian trajektorii.

Chaos w równaniach ruchu można wykryć numerycznie za pomocą tzw. wskaźników Lapunowa. Bada się mianowicie zależność od czasu różnicy dwóch trajektorii, początkowo bardzo małej. Ta różnica jest parametryzowana jako exp(at), gdzie a jest wskaźnikiem Lapunowa. Jeśli a>0, mamy do czynienia z chaosem.

Chaos nie występuje w układach, opisanych liniowymi równaniami ruchu. Na przykład rozwiązania równania dx / dt = ax nie uważamy za chaotyczne. Zwykle dyskutuje się przypadki, kiedy trajektoria jest ograniczona w przestrzeni.

Jednym z najsłynniejszych przykładów zachowania chaotycznego są rozwiązania równań Lorentza. Są to trzy nieliniowe równania różniczkowe pierwszego rzędu, skonstruowane z myślą o modelowaniu zjawisk atmosferycznych (o tym później).

Przypadkiem najprostszym jest równanie iteracyjne x(n + 1) = bx(n)[1 - x(n)], które przejawia chaos dla niektórych wartości parametru b. Równanie to jest znane jako równanie logistyczne, a używane w zagadnieniach rozwoju populacji w czasie.

Popularne doświadczenia

Jak już wcześniej wspomniałem Teoria Chaosu jest wszechobecna. Śledząc wysiłki fizyków na przestrzeni lat bardzo często można się spotkać z dwoma przykładami i dwoma nazwiskami:

Odkrycia tych obu badaczy były poprzedzone ogromną ilością pracy całej „armii” genialnych fizyków (choćby H.Poincaréego czy A. Kołomogorowa równania mechaniki nieba). Jednakże ich niepodważalnym sukcesem było udowodnienie chaotycznej natury w/w zjawisk. Dowody te były realne głównie dzięki zastosowaniu nowoczesnych metod numerycznych i bardzo szybkich komputerów. Nie znaczy to jednak, że wcześniej nie dało się tego osiągając. Po prostu złożoność obliczeniowa rosła wykładniczo stawiając przed badaczami nieprzebytą barierę czasu. Zastosowanie natomiast komputerów pozwoliło spojrzeć w dane zagadnienie z szerszego punktu widzenia. Przykładowo wyznaczenie czasu charakterystycznego dla ruchu planet zajęłoby parę pokoleń ciągłych obliczeń a maszyna zrealizowała to w bardziej realnym czasie.

Do analizy układu wykazującego charakter chaotyczny używa się specjalnie do tego zdefiniowanych pojęć. Powyżej wspomniałem o „czasie charakterystycznym”. Cóż to takiego? Układ chaotyczny jak wiemy wzmacnia odchylenia początkowe, więc czas charakterystyczny układu jest okresem po którym odchylenie to wzrasta dziesięciokrotnie. Dwie trajektoria odległe na początku o d będę po upływie czasu charakterystycznego odległe o 10d. Drugim ważnym pojęciem jest atraktor. Definiuje się go jako wyróżniony podzbiór możliwych stanów układu do którego nieuchronnie zmierza ewolucja układu. Najlepiej jednak to przestawić na przykładzie. Mając do dyspozycji wahadło, mocujemy je i puszczamy z dowolnego położenia. Wiemy, że pod wpływem sił tarcia (wahadło o powietrze oraz w zamocowaniu) zatrzyma się w końcu po jakimś trudno przewidywalnym czasie. Wiadomo również, że ten stan jest nieunikniony tj. osiągnięcie w/w stanu nie jest zdeterminowane prędkością początkową ani wartością wychylenia. Tak, więc to spoczynkowe położenie wahadła będzie dla tego układu atraktorem. W powyższym przykładzie atraktorem będzie konkretny punkt spoczynkowy jednak bardzo często spotyka się, że atraktory o skomplikowanej strukturze. Szczególną klasę stanowią atraktory dziwne. Odwołując się do trajektorii można je zdefiniować jako takie, które przyciągają trajektorie z zewnątrz a ruch w ich wnętrzu jest chaotyczny i nieprzewidywalny. Bardzo sławnym atraktorem rozbudzającym wyobraźnię naukowców od 1963r. (data publikacji) jest atraktor Lorenza. Jak już wcześniej wspomniałem zajmował on się metrologią i postępując z duchem teorii chaosu udało mu się uprościć bardzo skomplikowane równania opisujące zależności bardzo dużej liczby zmiennych. Wynikiem jego prac są (sławne już) trzy równania różniczkowe (już wspomniane). Pomimo, że bazą były badania metrologiczne same równania przez znaczne uproszczenie uzyskały pewien dystans od pierwotnych założeń. Tym nie mniej pozwoliło to zobrazować atraktor już na płaszczyźnie trzy wymiarowej.

Ruch w dziwnym atraktorze Lorenza jest chaotyczny: nie można przewidzieć, czy w kolejnym kroku trajektoria znajdzie się w jednej pętli, czy w drugiej.

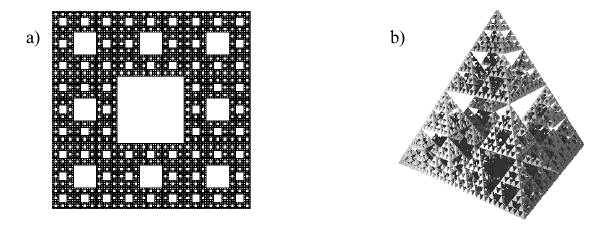
Poza „dziwnymi atraktorami” występują też atraktory samopodobne. W nich natomiast kształty stają się bardzo uporządkowane i systematyczne. Doskonałymi przykładami są fraktale.

Fraktalami (łac. fractus złamany) nazywamy zbiory geometryczne, dla których wymiar jest liczbą naturalną. Przykładowo, fraktalem o wymiarze równym stosunkowi logarytmu z 2 do logarytmu z 3 jest zbiór Cantora (podzbiór odcinka o wymiarze 1), a dywan Sierpinskiego (podzbiór kwadratu) stanowi fraktal o wymiarze ln8/ln3.

a) dywan Sierpińskiego o wymiarze D = ln8/ln3; b) piramida Sierpińskiego o wymiarze D = 2

Chaos a matematyka

Zanim jednak przytoczę matematyczną interpretację chaosu (dowody jego istnienia i jego implikacje) dwa słowa o symulacjach. Przecież ogólnie wiadomo, że układ chaotyczny działa jak „wzmacniacz” tj. mało wymiarowe różnice  po paru okresach charakterystycznych układu zaczynają odgrywać bardzo znaczącą role. Co jednak z symulacjami? Powszechnie wiadomo, że operacje matematyczne wykonywane przez komputer są tak naprawdę w jego pamięci zaokrąglane. Tu jednak wkracza wyżej wspomniany rozwój metod numerycznych w postaci lematu śledzenia. (W dużym uproszczenie udowadnia on, że te małe zaokrąglenia i błędy obliczeń wywołane nimi kompensują się.)

Definicja Devoney (1989r.)

1. topologiczna przechodniość ( T )
2. gęstość punktów okresowych ( P )
3. wrażliwość na zmianę danych początkowych ( S )

( T ) - rozrzucenie punktów po zbiorze

( P ) - w jaki sposób regularny (chaos jest w pewien sposób regularny - w pełni nieregularna jest losowość)

( S ) - mała zmiana powoduje ogromne efekty

(funkcja ciągła przekształcająca X w X, zadaje dynamikę / zmienność (kolejne rozrzuty, "stop klatki")

O (x) - orbita znajdująca się w x

(zbiór nieskończony)

Punkt nazywamy okresowym (periodycznym o okresie 

f ⁿ - n-ta iteracja funkcji n

W szczególności: punkt okresowy o okresie jeden nazywamy punktem stałym f(x)=x.

f ma własność( T ) dla dowolnej pary zbiorów otwartych (dowolnie małe otoczenie punktu, zbiory bez krańców) U i V istnieje

( P ) - w każdym przedziale istnieje co najmniej jeden punkt okresowy

f spełnia ( S ) istnieje , że dla każdego i każdego otoczenia Ux istnieje, istnieje (coś co było dowolnie blisko będzie w odległości większej niż delta, istnieje co najmniej jeden taki punkt)

f ma własność rozszerzalności ( E ) istnieje że dla każdego istnieje

Spełnienie ( E ) spełnienie ( S )

Banks, Brooks, Cairivs, Davis udowodnili

Wykazano także że , czyli chaos określa właściwość (T)

Ponadto wykazano: Punkt o okresie 3 implikuje istnienia chaosu

Każdy układ chaotyczny więcej niż 3 wymiarowy można dowolnie blisko przybliżyć układem trzy wymiarowy.

„Chaos” w Polsce

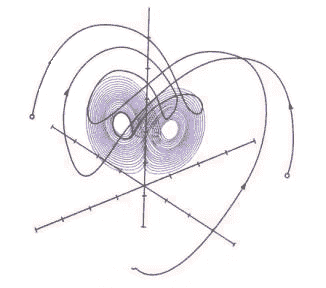
Teoria chaosu i układów dynamicznych uprawiana jest w Polsce z powodzeniem w różnych ośrodkach akademickich, a na organizowane konferencje przyjeżdżają wybitni uczeni z całego świata. W dniach 19–22 czerwca 2002 roku w Instytucie Matematyki Uniwersytetu Jagiellońskiego w Krakowie odbyła się konferencja „Geometric Theory of Dynamical Systems” a Instytut Biocybernetyki PAN w Warszawie zorganizował w okresie 18–27 czerwca konferencje „Euroattractor 2002”, poświecona dynamice nieliniowej i analizie sygnałów czasowych.

Konferencja Euroattractor, po raz trzeci organizowana w Warszawie, mimo swej nazwy przyciąga także naukowców spoza Europy. Nazwa ta zainspirowała zgromadzonych tam naukowców do poszukania układu dynamicznego, którego atraktor ma kształt zbliżony do konturów naszego kontynentu. Niezależnie od wyjściowego zbioru na płaszczyźnie, ewolucja układu w czasie dążyć będzie do zbioru przedstawionego poniżej w formie obrazu.

Euroatraktor: zbiór nie zmieniający się podczas ewolucji w czasie

Literatura:

„Chaos” Ivar Ekeland
”Chaos, fraktale i euroatraktro” K. Życzkowski, A. Łoziński

Internet:

Wykonał:

Małyska Sebastian
WTiE sem.V gr.7
sebam@go2.pl