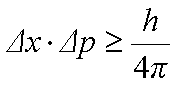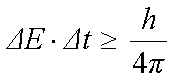Słowniczek pojęć kwantowych - spis treści

Zasada nieoznaczoności Heisenberga
    Zasada nieoznaczoności w ujęciu fizycznym
    Zasada nieoznaczoności w ujęciu ogólnym

Stany własne
    Stany własne w ujęciu fizycznym
    Stany własne w ujęciu psychologicznym

Operatory

Zasada nieoznaczoności Heisenberga

Zasada nieoznaczoności w ujęciu fizycznym

W ujęciu fizycznym zasada ta mówi że nie da się z dowolną dokładnością wyznaczyć dwóch wielkości których operatory ze sobą nie są przemienne  (czyli "nie komutują" - przepraszam za ten naukowy zwrot, ale trudno to napisać tak, żeby było jednocześnie i ściśle, i zrozumiale). Odnosi się ona m.in. do par takich wielkości jak:

	pęd i położenie
	energia i czas
	składowych momentu pędu cząstki

Matematycznie zasada ta wyraża się wzorem (h - stała Plancka, h = 6,62 · 10^-34 J·s)

Nieoznaczoność pędu i położenia

Nieoznaczoność czasu i energii

Zasada nieoznaczoności wyraża sobą prawdę, że najczęściej pomiar zakłóca stan mierzonego obiektu. Tylko wtedy, gdy obiekt znajduje się w stanie własnym operatora danego pomiaru (najczęściej w jednym z możliwych stanów własnych), możliwe jest uzyskanie jednoznacznej odpowiedzi na dany test – doświadczenie. Jeżeli zaś obiekt znajduje się w innym stanie niż własny, to proces pomiaru musi najpierw przekształcić go w stan własny operatora pomiaru (najczęściej jeden z wielu do wyboru stanów własnych). Bo jednoznaczną odpowiedź można uzyskać  tylko w jednym ze stanów własnych operatora wielkości mierzonej. Jednak to przekształcenie w stan własny jednego operatora wiąże się w wielu wypadkach z wyprowadzeniem obiektu ze stanu własnego innego operatora (operatora innej wielkości fizycznej, innego pomiaru), czyli z zakłóceniem tej innej wielkości. Wynika to z faktu, że w wielu przypadkach różne operatory (operatory odpowiadające różnym wielkościom pomiarowym) mają niezgodne stany własne.

Np. mierząc pęd elektronu, pomiar musi przekształcić funkcję falową elektronu w jeden ze stanów własnych operatora pędu. Jednak funkcja własna operatora pędu nie jest funkcją własną operatora położenia. Z kolei, aby zmierzyć położenie, musimy znowu przekształcić funkcję własną elektronu w jeden ze stanów własnych operatora położenia, wiąże się z następnym zaburzeniem stanu tej cząstki. Czyli gdy mierzymy położenie, tuż po zmierzeniu pędu, wtedy badamy już inną funkcję falową niż w poprzednim pomiarze. 

Zasada nieoznaczoności w ujęciu ogólnym

Sens zasady nieoznaczoności Heisenberga zawiera się w fakcie, że wykonywanie pomiaru zakłóca stan mierzonego obiektu. Dlatego jeżeli wykonujemy jednocześnie (lub tuż po sobie) dwa pomiary A  oraz B, a pomiar A zmienia właściwości związane ze stanem B, to uzyskane wyniki będą zaburzone.

Przykład z psychologii:

Załóżmy, że pomiar stanu szczerości księgowych w firmach realizujemy badając odpowiedź na następujące pytanie:

A.     Czy nie zdarzyło się Panu ukryć przed urzędem skarbowym jakieś dochody?

Z kolei jednocześnie chcielibyśmy zmierzyć stan poinformowania respondenta o warunkach pomiaru za pomocą pytania:

B.     Czy zdaje Pan sobie sprawę, że aktualne badanie realizowane jest przy współudziale pracowników urzędu skarbowego?

Tutaj operatory pomiarów „szczerości” i „poinformowania o badaniu” są nieprzemienne (nie komutują).  Jeśli najpierw spytamy się o A, to zapewne panika po udzieleniu szczerej odpowiedzi, każe w sposób „dziwny” zareagować na pytanie B. Oczywiste jest też, że po pytaniu B, niewielu respondentów ujawni swoją „nieskrępowaną szczerość”.

Ostatecznie można by wywnioskować, że nie da się dla tych samych respondentów wyznaczyć jednocześnie i „szczerości” (przynajmniej w jej ogólnym, niezakłóconym sensie) i „wiedzy o badaniu”.

Ten przykład można uogólnić - nierzadko przy wykonywaniu dwóch różnych pomiarów A i B będą one wpływały na swoje wyniki. I dlatego nie będzie można wyznaczyć tych obu wielkości jednocześnie.

Stany własne

Stany własne w ujęciu fizycznym

Obiekt znajduje się w stanie własnym operatora A, jeżeli efektem zadziałania tego operatora na obiekt będzie uzyskanie jednej, dobrze określonej liczby (nazwijmy ją wynikiem, lub wartością operatora) charakteryzującej dany stan.

Można to zapisać wzorem:

<operator A> [Obiekt] = wynik_A · [Obiekt]

Tutaj lewą stronę należy odczytać jako: „operator działa na Obiekt”, zaś wynik_A jest liczbą – wynikiem uzyskanym z pomiaru.

Jednak jeżeli Obiekt nie znajduje się w stanie własnym danego operatora, to powyższe „równanie” nie zachodzi, a obiekt trzeba będzie zapisać jako superpozycję stanów własnych operatora A:

[Obiekt] = udział_1 · [Obiekt w stanie 1 operatora A] + udział_2 · [Obiekt w stanie 2 operatora A] + udział_3 · [Obiekt w stanie 3 operatora A] +...

Równanie powyższe należy interpretować w ten sposób, że całkowity stan obiektu rozpada się na poszczególne stany własne operatora A. Cały stan obiektu składa się (jest superpozycją) z wielu stanów własnych operatora. Tutaj udziały_1, 2, 3 stanowią liczby od których zależy prawdopodobieństwo, że obiekt ujawni się w określonym stanie. Np. jeżeli udział_2 jest duży, to występuje duże prawdopodobieństwo, że obiekt znajdzie się w stanie 2. Jednak nie wiadomo na pewno który stan „wybierze sobie” obiekt podczas pomiaru. Składników tworzących całkowitą funkcję falową obiektu może być bardzo dużo – najczęściej nieskończenie wiele. Na szczęście w większości przypadków okazuje się że stan obiektu daje się rozbić na funkcje „ważniejsze” (te z dużymi udziałami), „mniej istotne”, a nawet „prawie nie mające wpływu” (z udziałami bardzo bliskimi zera). Wtedy te mało ważne funkcje można pominąć, i problem daje się „ugryźć” od strony matematycznej.

Dzięki operacji rozdziału obiektu na jego składowe stany pomiar A da się przedstawić schematem:

<operator A> [Obiekt] = wynik_A₁ · udział_1 · [Obiekt w stanie 1 operatora A] + wynik_A₂ · udział_2 ·  [Obiekt w stanie 2 operatora A] + wynik_A₃ · udział_3 · [Obiekt w stanie 3 operatora A] +itd...

Schemat ten należy interpretować tak, że w zależności od udziałów 1, 2, 3 itd. obiekt jako wynik pomiaru zaserwuje nam albo wynik_A₁, albo wynik_A₂, albo wynik_A₃, itd... (nigdy dwa czy trzy na raz!)  Im większy udział danego stanu, tym większe prawdopodobieństwo znalezienia się obiektu w stanie o danym numerze i wyprodukowania odpowiedniego wyniku. 

Stany własne w ujęciu psychologicznym

Można wyobrażać sobie, że stany własne są to jakby „czyste” zachowania obiektu. Mogą być one tworzone przez sytuacje, które wywołują w obiekcie zawsze taką samą reakcję.

Np. człowiek znajduje się w „stanie własnym strachu przed psem” jeżeli zawsze na widok psa będzie reagował tak samo.

Jednak u większości ludzi spotykamy różne reakcje na niebezpiecznego psa – raz reagują krzykiem, raz ucieczką, innym razem atakiem, czy spokojnym czekaniem. Można by powiedzieć, że stan reakcji na groźnego psa „składa się” ze stanów ucieczki, ataku, straszenia itd. Efekt spotkania z takim psem jest niejednoznaczny – mogą być wybrane zachowania spośród wielu dostępnych. Ogólnie więc stan w jakim znajduje się cokolwiek lub ktokolwiek „składa się” (jest jakby sumą) z wielu stanów prostych.

Stany własne obiektu są wygodne do badań i dlatego najczęściej naukowcy starają się doprowadzić, aby badanie przebiegało w warunkach stanu własnego. Wtedy otrzymany wynik jest jednoznaczny, czyli da się łatwo zinterpretować.

Niestety dość często jest tak, że stan prosty (własny) dla jednego typu zachowań - sytuacji nie jest już prosty dla innego typu sytuacji.

Przykład:

Wyobraźmy sobie, że chcemy skonstruować operator_skąpstwa.  Tym operatorem byłaby jakaś procedura pozwalająca nam powiedzieć jak bardzo skąpy jest człowiek (np. wyrazić jego skąpstwo na skali od 0 do 100). Jednak przy badaniu konkretnych ludzi okazuje się, że przejawiają oni swoje skąpstwo różnie w różnych sytuacjach – np. jeden jest skąpy głównie dla obcych, a dla rodziny dość hojny, inny, mimo wielkiej oszczędności przy kupowaniu ubrania, chętnie stawia piwo, jeszcze inny walczy o każdą złotówkę wypłaconą swoim pracownikom, ale przyjaciół zaprasza na fundowane przez siebie bankiety.

Dlatego sensownie skonstruowany operator skąpstwa, musiałby uwzględniać wszystkie składniki – czyli skąpstwo wobec rodziny, wobec pracowników, przyjaciół itd.

W tym kontekście (i oczywiście w sporym uproszczeniu) skąpstwo wobec pracowników byłoby pierwszym stanem własnym skąpstwa, skąpstwo wobec rodziny drugim stanem własnym tego operatora itd...

Całkowite skąpstwo wyznaczalibyśmy jak o sumę wszystkich składników skąpstwa...

 Jednak w konkretnej życiowej sytuacji przejawia tylko jeden rodzaj skąpstwa – np. jeżeli pracownik prosi rzeczonego skąpca o podwyżkę, to sytuacja wymusza wcielenie się w stan „skąpstwa pracodawcy”, jeżeli zaś córka skąpca ciągnie go do budki z lodami, to ujawniają się aspekty „skąpstwa rodzinnego”.

Każdy „czysty” rodzaj skąpstwa jest stanem własnym operatora skąpstwa, sytuacja życiowa przekształca obiekt w jeden ze stanów własnych.

Sytuacja czasami dosyć się komplikuje - np. jeżeli nasz skąpiec – pracodawca zatrudnił sobie kogoś z rodziny (załóżmy, że ten skąpiec dla rodziny jest dość szczodry, a z pracowników wydusiłby ostatni grosz). W sytuacji prośby tego rodzinnego pracownika o podwyżkę, może objawić się zarówno rodzinna hojność, jak też skąpstwo pracodawcy. Pracownik znający swojego chlebodawcę będzie więc rozważał: „na dwoje babka wróżyła – albo da podwyżkę bo jestem z jego rodziny, albo nie da, bo jestem pracownikiem...”

Operatory

W ujęciu matematycznym operator jest to po prostu pewna procedura przekształcająca jedną funkcję falową w inną funkcję falową.

Jednak fizycy najczęściej rozpatrują operatory, które są związane z pewnymi wielkościami – np. operator pędu działający na funkcję falową będącą w stanie własnym tego operatora „wyprodukuje” przy okazji swojego działania liczbę opisującą pęd obiektu. Podobnie operator położenia da, po zadziałaniu, liczbę stanowiącą o położeniu obiektu.

W odniesieniu do rzeczywistości operatory symbolizują doświadczenia, działania jakie wykonujemy z obiektem – np. operator pędu będzie związany z doświadczeniem polegającym na pomiarze pędu.

Działanie operatora nie jest dla funkcji falowej „obojętne”. Operatory po zadziałaniu (czyli po wykonaniu pomiaru) przekształcają funkcję falową w jeden ze swoich stanów własnych, czyli zaburzają stan obiektu.

W ujęciu ogólnym operator też mógłby symbolizować po prostu cechę jaka wiąże się z obiektem. Jednocześnie działanie operatora na sytuację, to po prostu interakcja z tą sytuacją – np. można powiedzieć, że policjant działa na kierowcę samochodu operatorem „zatrzymania go do kontroli”, a zakochana dziewczyna działa na swojego chłopaka "operatorem pocałunku"...